多个样本的均值比较
ANOVA:方差分析
在进行多个样本的均值比较的时候,没有办法使用原先的t检验方法。此时应当使用方差分析,来判断是否至少有一个总体的均值与其他总体不同(即各组总体均值不全相等)。方差分析的核心思想是:将所有分组的样本混合并计算方差得到总变异度SST,通过数学变换可以将总变异度拆分成两个成分,即组内变异SSW与组间变异SSG。总变异度相同时,各个总体之间的均值差距越大,则SSG便越大,而SSW越小;SSG与SSW的比值也会越大。当 $\frac{SSG}{SSW}$ 大到一定程度,我们便拒绝虚无假设H0,认为至少有一个总体的均值与其余总体不同。
假设有如下的K个总体:
|
总体1 |
总体2 |
总体3 |
…… |
总体K |
| 均数 |
$\mu_1$ |
$\mu_2$ |
$\mu_3$ |
…… |
$\mu_K$ |
| 方差 |
$\sigma_1^2$ |
$\sigma_2^2$ |
$\sigma_3^2$ |
…… |
$\sigma_K^2$ |
样本组 $i$ 从总体 $i$ 中抽出 $n_i$ 个样本,每个样本记为 $x_{ij}$ 。每个样本组的样本数可相同可不相同:
|
样本组1 |
样本组2 |
样本组3 |
…… |
样本组K |
| 样本数$n_i$ |
$n_1$ |
$n_2$ |
$n_3$ |
…… |
$n_K$ |
| 样本和$x_{i.}$ |
$x_{1.}$ |
$x_{2.}$ |
$x_{3.}$ |
…… |
$x_{K.}$ |
| 样本均数$\bar{x_i.}$ |
$\bar{x_{1.}}$ |
$\bar{x_{2.}}$ |
$\bar{x_{3.}}$ |
…… |
$\bar{x_{K.}}$ |
检验假设前提是否满足
ANOVA分析的前提假设需要所有总体的方差相等,即$\sigma_1^2\ =\ \sigma_2^2\ =\ \sigma_3^2\ =\ ...\ = \sigma^2$。我们假设各组间方差没有差异,或差异至少不要太大。
确定假设
- H0:$\mu_1\ =\ \mu_2\ =\ \mu_3\ =\ ...\ = \mu_K$,个总体的均值均相等。
- H1:至少有一个总体的均值与其它总体的均值不同。
构建检验统计量
1、计算SST、SSW与SSG:
$$
SST\ = \ \sum_i^K{\sum_j^{n_i}{(y_{ij}-\bar{y_{..}})^2}}\\
=\ \sum_i^K{\sum_j^{n_i}{y_{ij}^2}-2y_{ij}\bar{y_{..}}+\bar{y_{..}}^2}\\
=\ ......\\
=\ [\sum_i^K{\sum_j^{n_i}{y_{ij}^2-2y_{ij}\bar{y_{i.}}+\bar{y_{i.}}^2}}]\
+[\sum_i^K{n_i\bar{y_{i.}}^2-2n_i\bar{y_{i.}}\bar{y_{..}}+n_i\bar{y_{..}}^2}]\\
=\ \sum_i^K{\sum_j^{n_i}{(y_{ij}-\bar{y_{i.}})^2}}\ +\ \sum_i^K{n_i(\bar{y_{i.}}-\bar{y_{..}})^2}\\
=SSW\ + \ SSG
$$
其中,SST是总变异度,计算方式是将所有组的样本混在一起,计算总的方差;SSW是组内误差,即计算每组的方差再相加;SSG是组间误差,即计算每组的均值与总方差的差值的平方,乘以每组的样本数后相加。每个值都可以根据数据计算出对应值,不过根据上述公示推导得出:SST恰好是SSW和SSG之和,也就是说算出其中两个,就可以直接计算出第三个值。
2、构建检验量统计量 $F$
统计学得出,SSG服从自由度为K-1的卡方分布,SSW服从自由度为n-K的卡方分布(并非显而易见,证明过程十分复杂),故可以构建统计量$F$:
$$
F= \frac{\frac{SSG}{K-1}}{\frac{SSW}{n-k}} \sim F(K-1,n-K)
$$
发现F服从第一个自由度为K-1,第二个自由度为n-K的F分布。
计算P值
根据实验数据计算出F,然后查对应自由度的F表即可得到P值。
结果判定
如果P大于阈值,则得出结论:“没有足够的证据证明各组均值不完全相等”;如果P小于阈值,则说明至少有一组的均值与其他组均值相异,可以进行后续分分析来找出到底是那一组或哪几组存在异常。
方差分析的后续检验
如果方差分析差异显著,则可以使用“多重比较法”来找出哪一组或哪几组和其它组间有显著差异。多重比较法有数十种方式,可以根据需要进行选择。常见的多重比较法如下表所示:
| 多重比较法 |
适用场景 |
说明 |
| LSD法 |
使用最为广泛的多重比较法,组别较少时可以选用 |
最为敏感 |
| scheffe法 |
适用于各组别样本数量不相等的情况 |
较为保守 |
| Tukey法 |
较为通用 |
计算较为简便,适合手算 |
| Duncan法 |
用于多个均数的两两比较,常用于探索性研究 |
- |
下面以Tukey法(最小显著差异法,Minimum Significance Difference(MSD))为例:
使用Tukey法进行多重比较
Tukey法的核心是:从相同正态分布的K个总体中依次抽出一个大小为n的样本,将最大的均数与最小的均数相减,再除以总体标准误可得:
$$
q=\frac{\lvert\bar{x}_{max}-\bar{x}_{min}\rvert }{\frac{S}{\sqrt{n}}}
$$
其中S是将所有K组样本合并后的标准差,则q服从k=K,自由度为n-K的学生化范围分布(Studentized range distribution),其概率密度函数为:
$$
f(x, k, \nu) = \frac{k(k-1)\nu^{\nu/2}}{\Gamma(\nu/2)2^{\nu/2-1}} \int_{0}^{\infty} \int_{-\infty}^{\infty} s^{\nu} e^{-\nu s^2/2} \phi(z) \phi(sx + z) [\Phi(sx + z) - \Phi(z)]^{k-2} \,dz \,ds
$$
其中$\phi(x)$和$\Phi(x)$分别是标准正态分布的概率密度函数与概率分布函数。
由此,如果q值大过了某个阈值,则拒绝原假设,认为两总体的均值不相等。这个阈值可以通过查表,或使用计算机程序很方便的得到。以下是Tukey法的具体步骤:
1、计算任意两组之间的平均数差异。有K个组别就要计算$n\choose2$次:
$$
d_{ij}=\lvert \bar{x_{i.}}-\bar{x_{j.}}\rvert,i≠j
$$
2、计算各组样本数的调和平均数:
$$
n^*=\frac{K}{\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}+...\frac{1}{n_K}}
$$
3、计算临界值MSD:
$$
MSD=Q_{\alpha,(K,n-K)}\sqrt{\frac{MSW}{n^*}}
$$
其中MSW即$\frac{SSW}{n-K}$,即组内变异除以n-K。$Q_{\alpha,(K,n-K)}$可以通过查Q表得到。
4、比较所有的$d_{ij}$,只要大于临界值MSD,则表示该两组的平均数之间有显著差异。
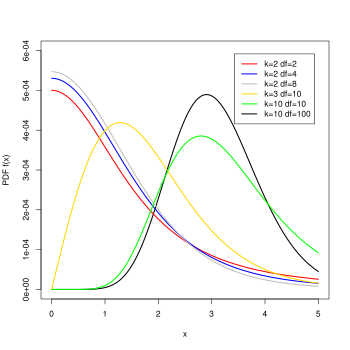
5、使用画图法进行分组。将K组按照均值大小降序排列。如果两组之间的均数差值未达阈值,就在下方用横线连接二者,反之不用划线。如下例所示,BC、CD、BD以及DE之间均数无显著差异,故在下方用横线连接。此时将所有相连的组分为一类,发现BCDE连在一起,而A与其余的不相连,故认为A的均值与其他组有显著差异。