批次效应与多样本整合
批次效应(batch effect),指样品在不同批次中处理和测量产生的与试验期间记录的任何生物变异无关的技术差异。不同时间、不同操作者、不同试剂、不同仪器导致的实验误差,反映到细胞基因的表达量上就是批次效应。批次效应可以很小,但也可能很大,甚至导致各个批次之间的数据完全无法比较。因此,在整合多个样本的数据时,需要通过一系列的算法减少批次效应带来的影响,使得各个批次之间具备可比性。
一个简单的例子
假设要对200名学生进行体检,测量他们的身高。现在一共有两位医生,每人测量100名学生,测量结果如下:
|
医生1测量结果 |
|
医生2测量结果 |
| 学生1 |
173.5281 |
学生101 |
185.6495 |
| 学生2 |
170.8003 |
学生102 |
175.9567 |
| 学生3 |
171.9575 |
学生103 |
176.1885 |
| …… |
…… |
…… |
…… |
| 学生99 |
170.2538 |
学生199 |
186.4897 |
| 学生100 |
170.804 |
学生200 |
184.0096 |
以医生1的测量结果为横坐标,医生2的测量结果为纵坐标画出散点图;同时将二者都由小至大排序后再画出散点图(类似Q-Q分位图):



此时发现医生1的所有测量结果的均数大约是170左右,而医生2的所有测量结果的均数大约是180左右,二者的方差也不一致。然而我们假设学生身高是来自同一个总体的,而且每个学生由哪位医生测量也是随机的,则理论上两位医生测量得到的平均身高应当较为接近,不可能差距10cm之多。
事实上,由于两位医生的测量方式、读数方式以及使用的卷尺质量如何都存在一定的差异,导致对学生身高的测量产生了误差,这种误差便是所谓的“批次效应”。尽管每个批次内的数据仍然是可比的,批次效应却使得两个批次之间的数据无法进行比较(由医生2测得的180cm身高不一定就比医生1测得的175cm要高)。如果不去除批次效应就对数据进行分析的话很有可能会得到错误的结论。
对于本例而言,一个简单的去除批次效应的方法就是线性缩放(Linear Scaling):我们期望两个批次的每个百分比的分位数都要近似相等,即在分位图上的点要尽可能地落在$y=x$直线附近。于是我们对现有的分位图进行线性拟合,拟合结果为$y=1.52278x-78.8095$
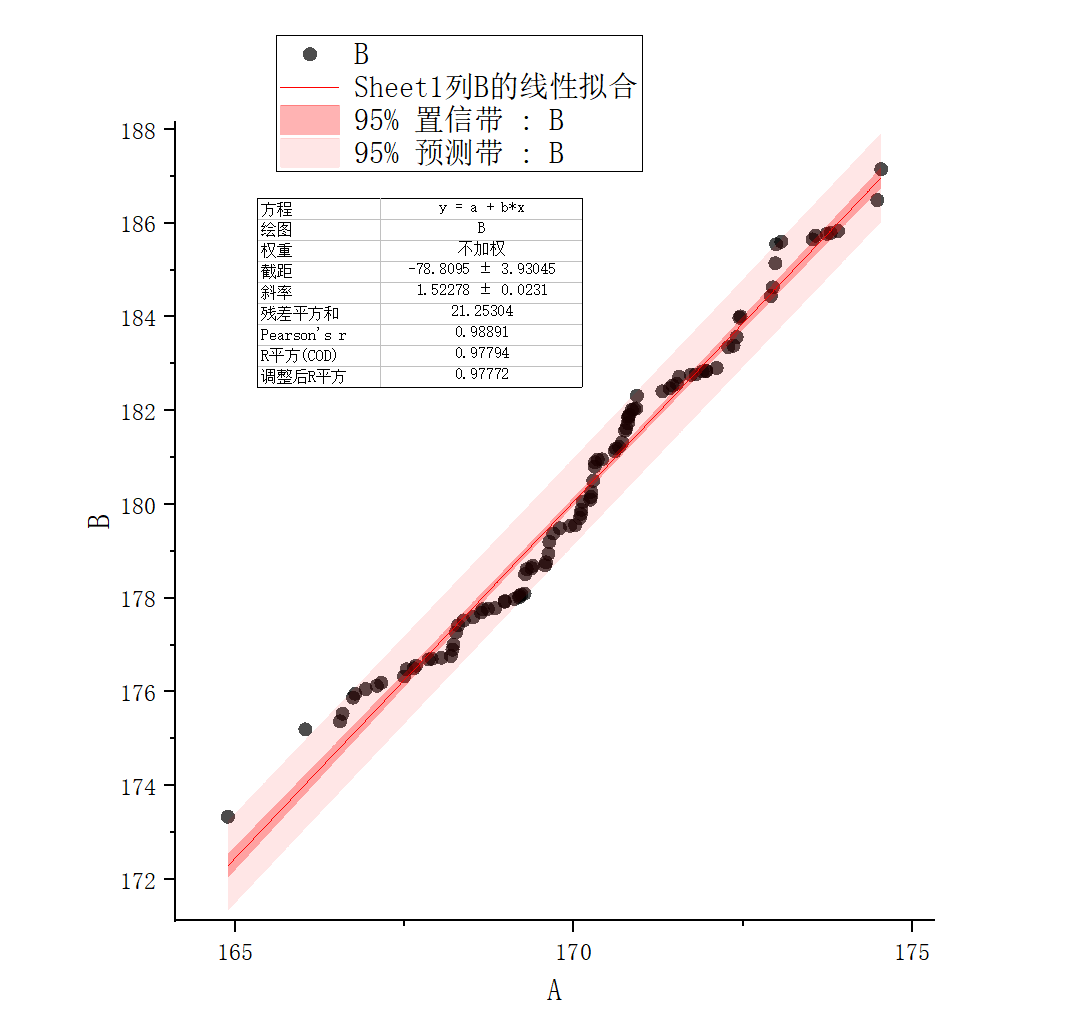
于是对医生2的测量数据进行线性放缩:
$$
y_{scaled} = \frac{y+78.8095}{1.52278}
$$
放缩后的分位图如下,此时两个批次的平均数已经缩放为一致的,并且方差相近,在一定程度上可以互相比较了:


导致批次效应的可能因素与实验设计
从标本获取、标本处理、测序、后续分析中任何非生物学因素都会导致批次效应,包括但不限于:
- 实验的时间差异
- 使用不同生产批次、公司的实验耗材、酶、抗体等
- 使用不同公司的实验动物
- 不同的实验员
- 不同批次的测序
- ……
矫正批次的算法都要求不同批次之间至少有一定程度的相同的部分。这要求我们在实验设计的时候需要避免“完美混杂”的情况,即不同类别的样本在处理过程中需要分散在不同批次里,例如,所有正常标本让一个实验员处理,而所有肿瘤标本让另一个实验员处理;或者所有的肿瘤标本都在某一批次的测序中。这样程序便无法判断基因表达的差异是由批次效应产生的,还是由生物学效应产生的了。
去除批次效应的算法
BBKNN
BBKNN的基本假设
BBKNN(Batch Balanced K-Nearest Neighbors,批次平衡K临近)是一种用于单细胞RNA测序数据整合的算法,专门设计来校正批次效应。其核心前提假设是:不同批次之间相同种类细胞的基因表达差异要小于相同批次的不同种类细胞之间的基因表达差异,即批次效应带来的影响应当小于细胞类型之间的差异。
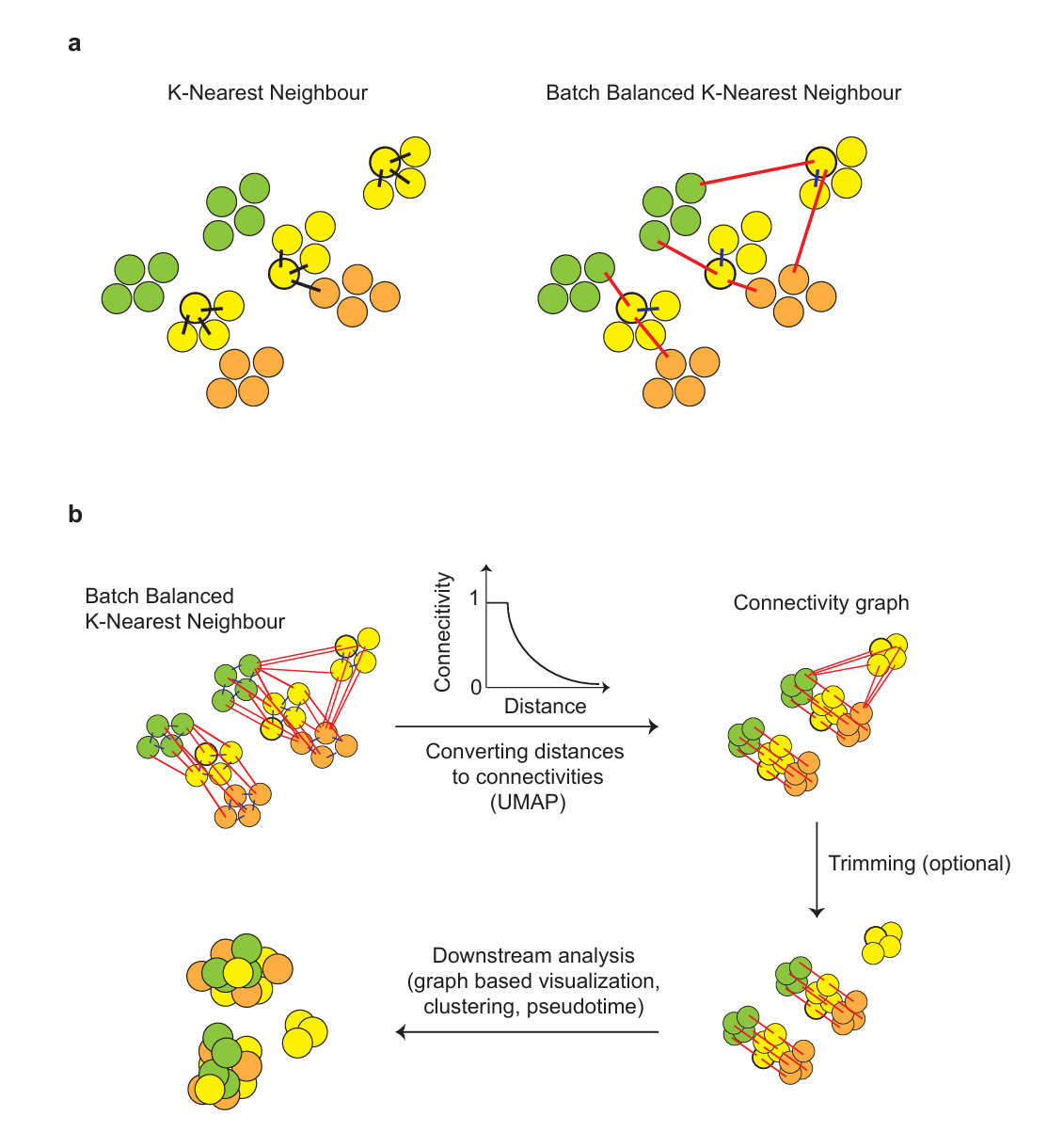
BBKNN的计算过程
1、归一化后取对数,消除测序深度以及偏态分布带来的影响:
设$x_{gc}$指基因g在细胞c中的counts(UMI计数),则:
$$
y_{gc}=log(1+\frac{x_{gc}}{\sum_g x_{gc}}\times scale\_factor)
$$
缩放因子scale_factor默认为10000。
2、对处理后的表达矩阵进行主成分降维,每个细胞在主成分空间内的坐标为$\pmb{z_c}$
3、对每个细胞,计算其在每个批次中的k个最接近的邻居:
$$
S_{bc}=\{a|a\in C_b,d(\pmb{z_c},\pmb{z_a}) \le \delta_{bc}\}
$$
其中:
$S_{bc}$指细胞c在批次b细胞中的最近k个邻居集合
$C_b$指批次号为b的细胞集合
$d(\pmb{z_c},\pmb{z_a})$即细胞c和细胞a在主成分空间内的距离
$\delta_{bc}$指批次为b的所有细胞中离细胞c第k近的细胞与细胞c之间的距离
4、对所有批次的k近邻取交集:
细胞c的所有邻居$Sc$为:
$$
S_c=S_{b_0c}\cup S_{b_1c} \cup S_{b_2c}\cup ...\cup S_{b_{N_{b}}c}
$$
在理想情况下我们希望$Sc$中所有细胞都是同一类型的。然而事实上总有非本类型的细胞被错误地纳入了$S_c$中,需要进一步优化。
5、计算连接分数$\alpha$,这一步与UMAP的处理类似:
$$
\alpha_{ca}=exp(-\frac{d(\pmb{z_c},\pmb{z_a})-\rho_c}{\sigma_c})
$$
其中:
$\rho_c=min(d(\pmb{z_c},\pmb{z_a})),a\in Sc$
选择合适的$\sigma_c$以满足$\sum_{a\in S_c}\alpha_{ca}=\lambda log_2(|S_c|)$,$\lambda$默认为1,其大小控制连接分数随距离增大而衰减至0的速度
6、将连接分数对称化:
$$
\omega_{ca} = \omega_{ac} = \alpha_{ac}+\alpha_{ca}-\alpha_{ac}\alpha_{ca}
$$
7、对$S_c$进行修剪,去除不正确的k近邻,记为$T_c$:
$$
T_c=\{ \alpha |\alpha \in S_c,\omega_{ca} \ge \epsilon_c \}
$$
其中:
$\epsilon_c$是细胞c与$S_c$中的细胞的连接分数中第t大的值(即保留前t个连接分数最大的细胞)
至此便得到了每个细胞在考虑了批次效应后的t个近邻,通过构建的t临近图可以代替原先的k临近图进行下游分析。
原始论文:BBKNN.pdf
combat
combat的基本假设
combat算法假设批次效应表现为一种非生物学因素的系统性的误差,会系统性地影响一个批次中基因表达量的均值和方差。对于批次 i 中样本 j 的基因 g 的表达量$Y_{ijg}$,存在如下关系:
$$
Y_{ijg} = \alpha_g+\pmb{X_{[g,:]}}\pmb{\beta_g}+\gamma_{ig}+\delta_{ig}\epsilon_{ijg}
$$
其中:
$\alpha_g$:是基因g的总体表达量(所有细胞表达的平均值),即本底表达量
$\pmb{X}$:是样本的设计向量,体现了该样本的与基因g表达有关的生物学信息(特征),以及批次效应信息。
$\pmb{\beta_g}$:是对应的回归系数。$\pmb{X}\pmb{\beta_g}$即为:因该样本的生物学特性导致的基因的表达量
$\gamma_{ig}$:第i个批次对基因g的加法效应
$\delta_{ig}$:第i个批次对基因g的乘法效应
$\epsilon_{ijg}$:随机误差项,$\epsilon_{ijg}\sim N(0,\sigma_g^2)$
则通过样本估算这些参数的值,就可以修正批次效应带来的影响:
$$
Y_{ijg}^\star = \frac{Y_{ijg}-\hat{\alpha_g}-\pmb{X_{[g,:]}}\hat{\pmb{\beta_g}}-\hat{\gamma_{ig}}}{\hat{\delta_{ig}}}+\hat{a_g}+\pmb{X_{[g,:]}}\hat{\pmb{\beta_g}}
$$
combat的计算过程
1、构建设计矩阵:
- 指定adata.obs中对应批次的列,将其转为one_hot编码,作为设计矩阵的第一部分
- 对于其它的列,如果是分类变量,则转化为dummy编码,作为设计矩阵的第二部分
- 对于其它的列,如果是数值变量,则直接保留原始数值,作为设计矩阵的第三部分
$$
\pmb{X} = (\pmb{batch}, \pmb{non\_numerical},\pmb{numerical})_{(\sum_in_i)\times p}
$$
其中$n_i$指批次$i$的细胞数量,假设一共有m个批次,p是设计矩阵的列数。
2、标准化数据:
- 由最小二乘法估算$\beta$。这里$\pmb{Y}$就是$\pmb{(adata.X)^T}$:
$$
\pmb{\hat{\beta}}=(\pmb{X}^T\pmb{X})^{-1}\pmb{X}^TY
$$
- 计算批次效应对基因表达量的平均加法影响(根据各批次细胞数量计算加权平均)。这里$ \pmb{\hat{\beta}}_{[:m,:]}$即$ \pmb{\hat{\beta}}$的前m行,即与设计矩阵中批次效应对应的onehot编码对应的系数矩阵;G是基因的数量。
$$
\pmb{\mu_{grand}}_{(1\times G)}=\frac{(n_1,n_2,...,n_m)_{1\times m}\cdot \pmb{\hat{\beta}}_{[:m,:]}}{\sum_in_i}
$$
- 计算标准化均值。标准化均值即由批次效应带来的平均偏移量加上由生物学因素造成的基因表达量。式中$(\pmb{0},\pmb{X}_{[,m+1:]})$就是将$\pmb{X}$的前m列(编码批次效应的列)的元素全设为0(不考虑批次效应的影响)。
$$
\pmb{\mu_{std}}_{(\sum_in_i)\times G}=\pmb{1_{(\sum_in_i)\times 1}}\times \pmb{\mu_{grand}}+(\pmb{0}_{(\sum_in_i)\times m},\pmb{X}_{[,m+1:]})\pmb{\hat{\beta}}
$$
- 计算池化方差。这里**2指对矩阵中每个元素进行平方运算
$$
\pmb{\sigma_{pooled}^2} = (\frac{1}{\sum_in_i},\frac{1}{\sum_in_i},...,\frac{1}{\sum_in_i})_{1\times \sum_in_i}\times [(\pmb{Y}-\pmb{X}\hat{\pmb{\beta}})** 2]
$$
则最终可以将$\pmb{Y}$标准化:
$$
\pmb{Y_{std,g}}=\frac{\pmb{Y_{[:,g]}}-\pmb{\mu_{std,g}}}{\sqrt{{\sigma_{pooled,g}^2}}}
$$
3、参数估计
记$\pmb{Y_{std}}=\pmb{Z}$,则:$Z_{ijg}\sim N(\gamma_{ig},\delta_{ig}^2)$,并且我们假设:
$\gamma_{ig}\sim N(Y_i,\tau_i^2)$,$\delta_{ig}^2\sim Inverse Gamma(\lambda_i,\theta_i)$
则可以根据标准化后的数据,通过距估计估计出$\gamma_i,\tau_i^2,\lambda_i,\theta_i$。之后再使用经验贝叶斯估计(EB估计)估计出$\gamma_{ig}$和$\delta_{ig}$(详细过程略,详情可以查看原始论文的补充材料)。
4、计算出纠正批次效应之后的基因表达量
$$
Y_{ijg}^\star = \frac{Y_{ijg}-\hat{\alpha_g}-\pmb{X_{[g,:]}}\hat{\pmb{\beta_g}}-\hat{\gamma_{ig}}}{\hat{\delta_{ig}}}+\hat{a_g}+\pmb{X_{[g,:]}}\hat{\pmb{\beta_g}}
$$
至此,我们便获得了矫正批次后的表达矩阵。
原始论文:Combat
此外,Combat-seq方法是对Combat的改进,相较于ComBat假设的高斯分布,它选择了更适合计数数据的负二项分布进行建模。计算方法复杂,可以参考原文献。
原始论文:Combat-seq.pdf
Harmony
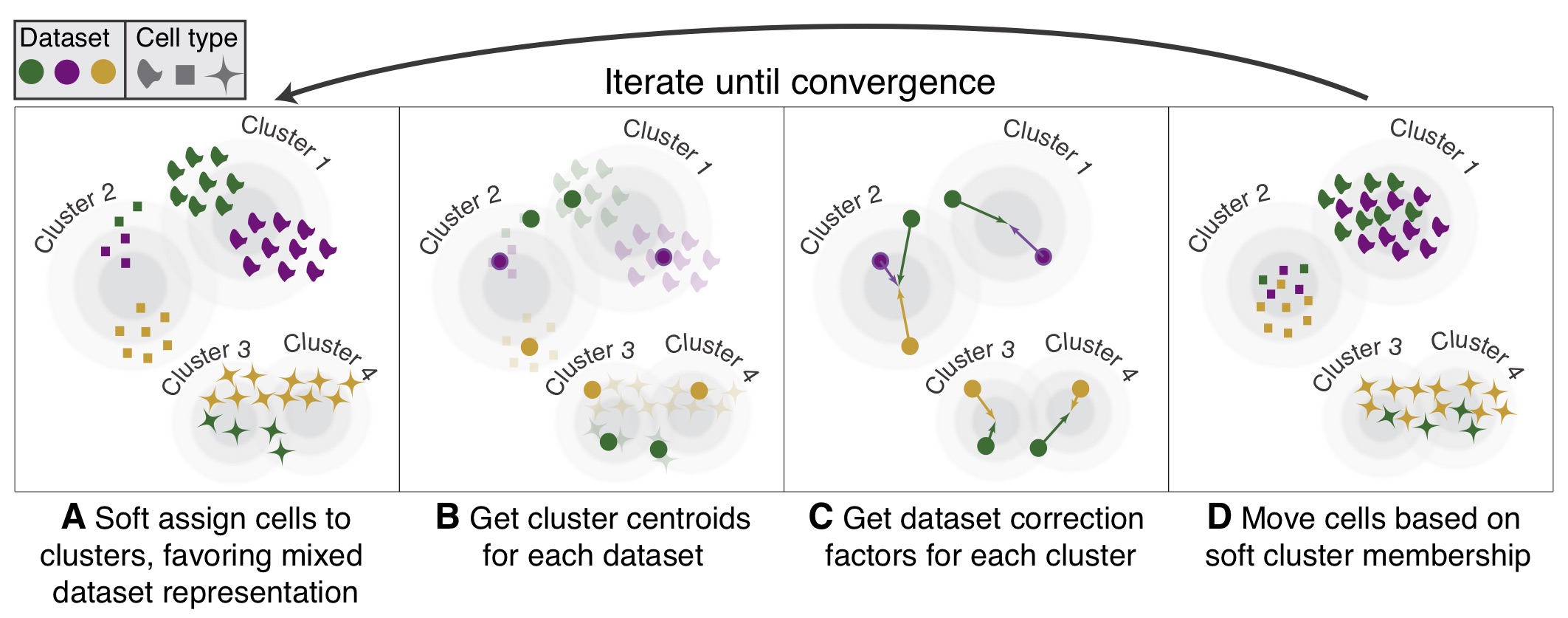
算法简述
Harmony算法基于主成分空间内的坐标值进行批次效应的去除:首先使用soft k-means clustering算法将细胞模糊聚类,然后计算每个cluster内各个数据集的细胞的中心点,然以及各个cluster的总体中心点。对于每个cluster,将每个数据集都向其总体中心点移动,然后反复重复上述三个步骤直至聚类效果趋于稳定。Harmony算法不设计原始的表达矩阵,而是对细胞的主成分坐标进行修改。
原始论文:Harmony
Scanorama
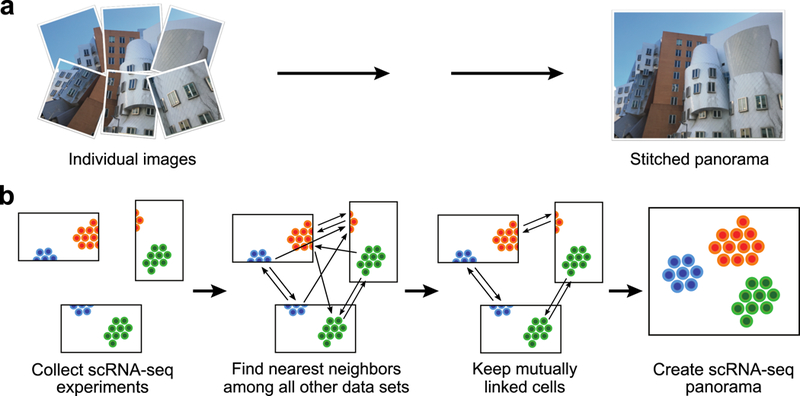
算法简述
全景图拼接算法通过寻找并合并重叠图像,生成一个更大、合成的图像。类似的策略也可用于整合异质的单细胞RNA测序数据集。Scanorama通过搜索最近邻,识别所有数据集对中共享的细胞类型。该过程利用降维技术和一种基于超平面局部敏感哈希与随机投影树的近似最近邻算法,大大加快了搜索速度。相互链接的细胞形成匹配点,可用于批次效应校正,并将不同实验合并(见方法部分)。在这些匹配基础上形成连通分量的数据集被整合为一个scRNA-seq“全景图”。
原始论文:scanorama
去批次实例
数据准备
在10xGenomics官网上下载两个数据集,分别是小鼠大脑矢状面切片的前端和后端:
V1_Mouse_Brain_Sagittal_Anterior -Datasets -Spatial Gene Expression -Official 10x Genomics Support
V1_Mouse_Brain_Sagittal_Posterior -Datasets -Spatial Gene Expression -Official 10x Genomics Support
预处理
进行基本的预处理工作,内容同上一节:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
# 导入相关库
import os
import scanpy as sc
import anndata as an
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import scanorama
sc.logging.print_versions()
sc.set_figure_params(facecolor='white',figsize=(8,8))
sc.settings.verbosity = 3
# 读取数据,即每个样本的outs/文件夹,这里原始数据已经被读入并保存为为h5ad文件。故直接读取。
adata_spatial_anterior = sc.read('adata_spatial_anterior.h5ad')
adata_spatial_posterior = sc.read('adata_spatial_posterior.h5ad')
# 使基因名唯一
adata_spatial_anterior.var_names_make_unique()
adata_spatial_posterior.var_names_make_unique()
# 首先分别进行标准化与取对数(而不是合并之后再标准化)
sc.pp.normalize_total(adata_spatial_anterior,inplace=True)
sc.pp.log1p(adata_spatial_anterior)
sc.pp.normalize_total(adata_spatial_posterior,inplace=True)
sc.pp.log1p(adata_spatial_posterior)
# 【关键步骤!】将两个样本合并。
# 两个样本的var_names(基因名)集合虽无需完全相同(程序会自动地将确实地基因用NaN来标记),
# 但是为了防止下游分析出现问题还是要预先对二者基因集取交集.
# 此外,var_names的顺序无需一致,程序会自动对齐.
# 这里两个对象的基因集已经是取过交集之后的结果,故在此不另作取交集操作。
adatas = [adata_spatial_anterior,adata_spatial_posterior]
adata = sc.concat(
adatas,label='batch',
uns_merge='unique',keys=[
k
for d in [
adatas[0].uns['spatial'],
adatas[1].uns['spatial'],
]
for k,v in d.items()
],
index_unique='-'
)
# 归一化,对数化筛选出高变基因
sc.pp.highly_variable_genes(adata,flavor='seurat',n_top_genes=2000)
# 备份,然后删去非高变基因
adata.raw = adata
adata = adata[:,adata.var.highly_variable]
# pca降维,构建邻域图,构建umap图,leiden聚类
sc.pp.pca(adata,svd_solver = 'arpack')
sc.pp.neighbors(adata)
sc.tl.umap(adata)
sc.tl.leiden(adata,key_added='clusters',resolution=1)
#### 可视化 ####
# umap
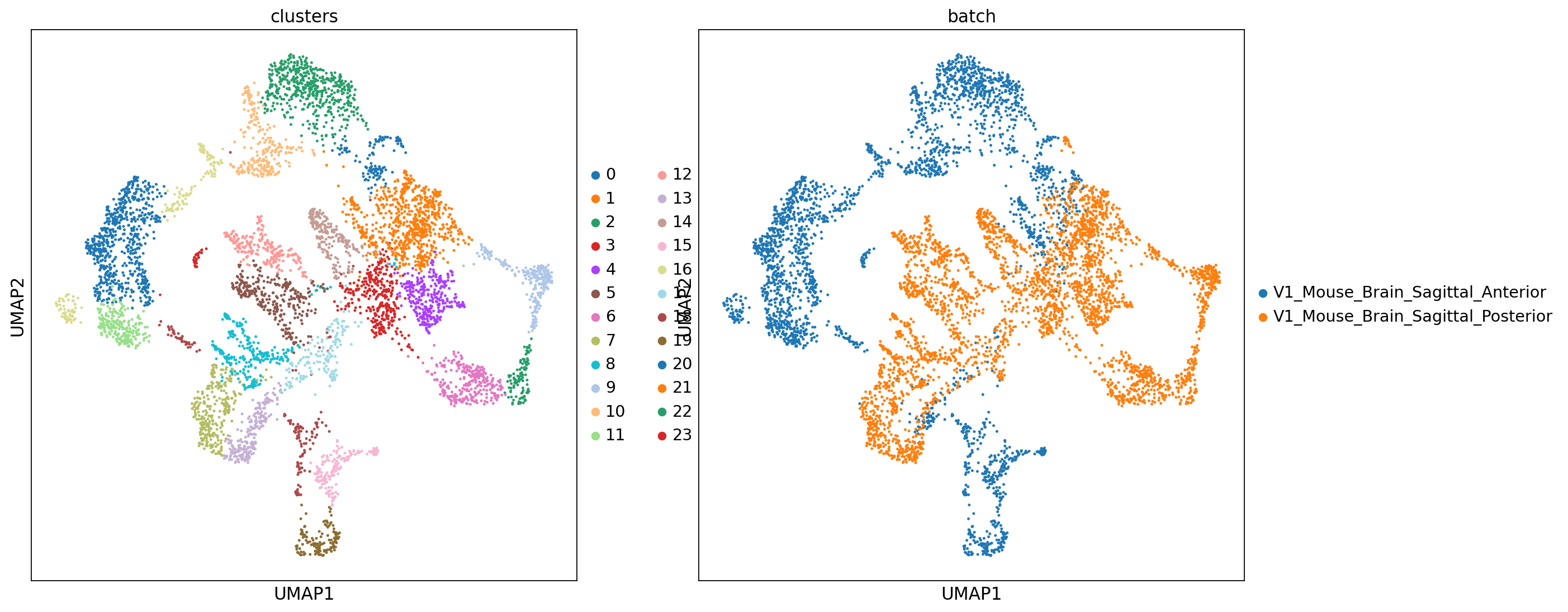
sc.pl.umap(adata,color=['clusters','batch'],palette=sc.pl.palettes.default_20)
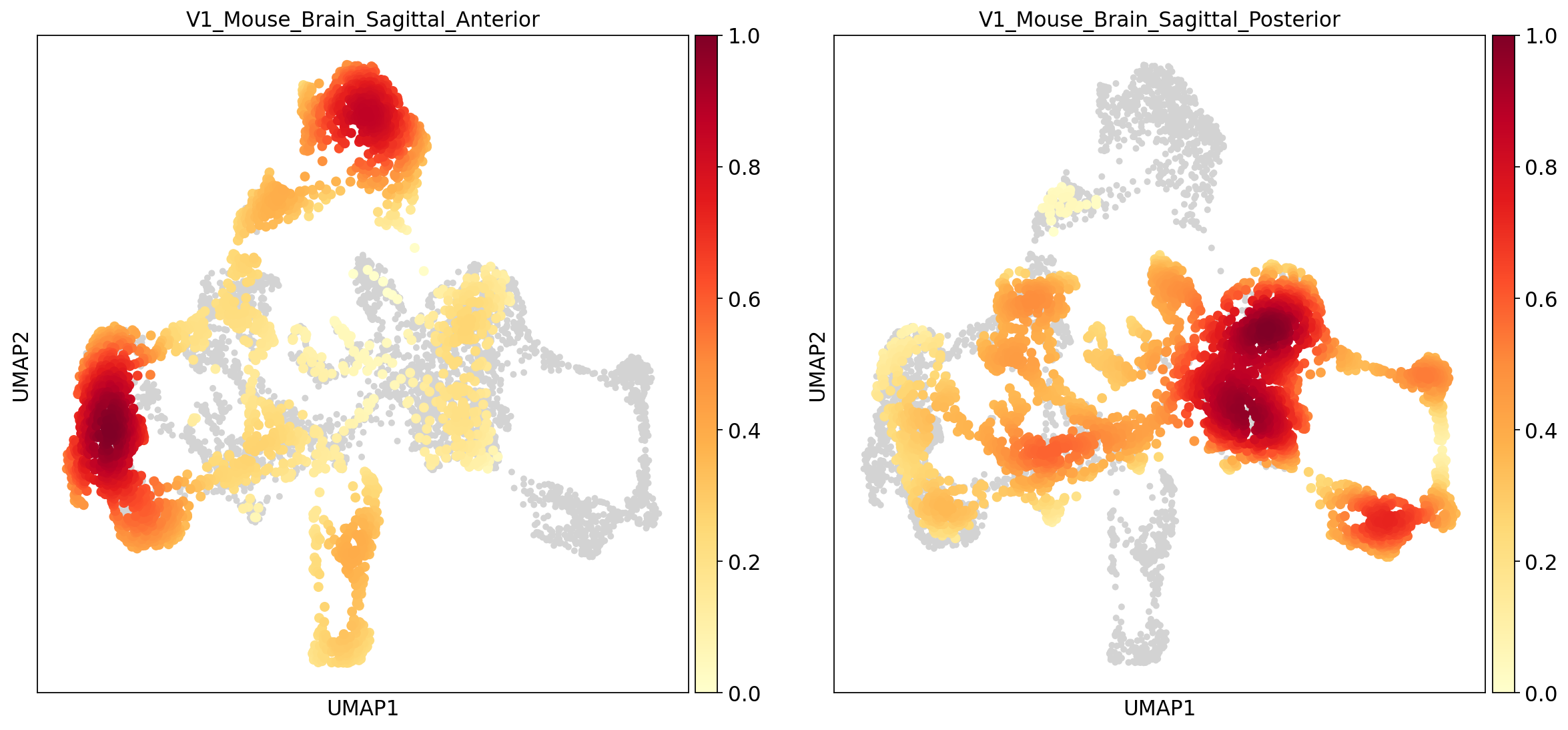
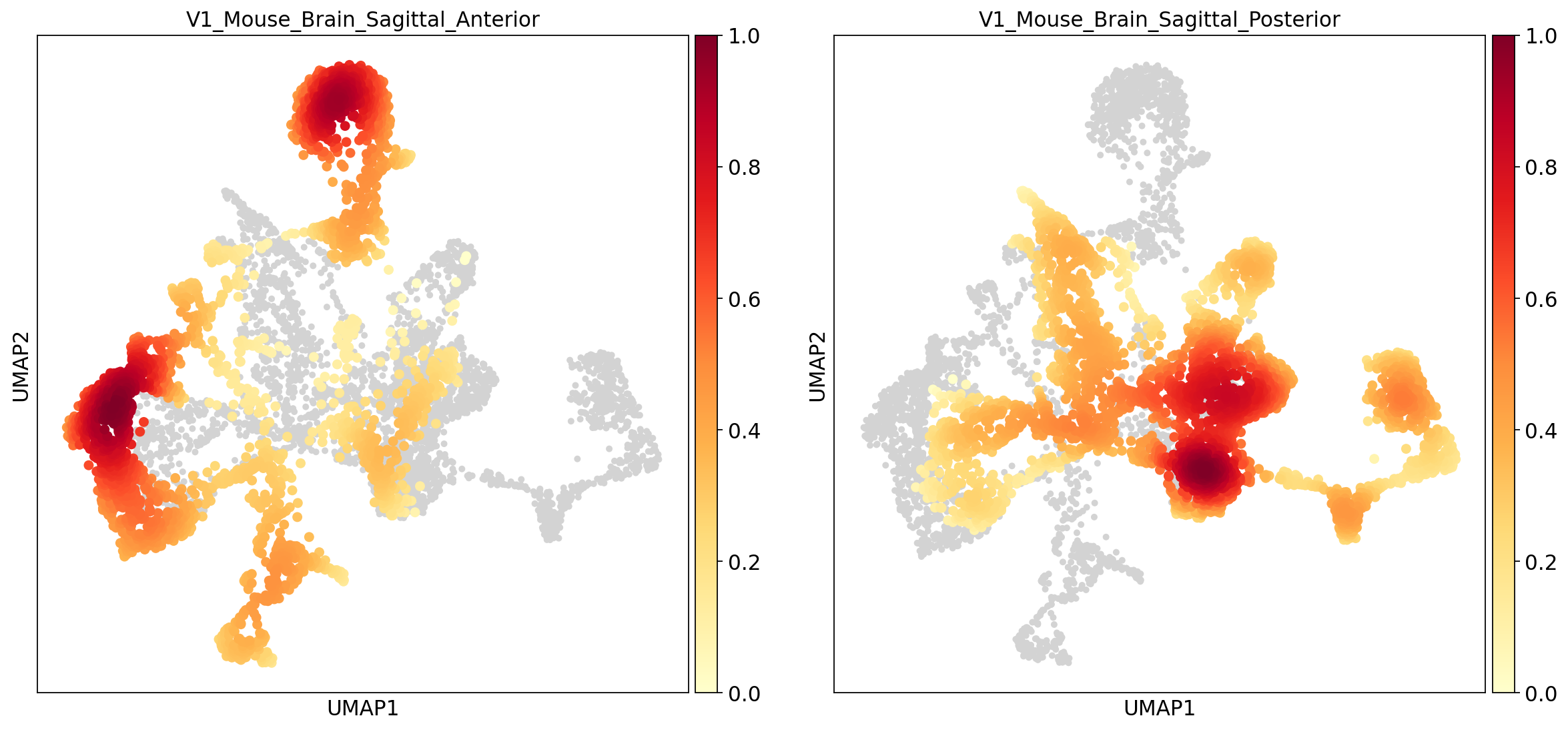
# embedding_density
sc.tl.embedding_density(adata,groupby='batch')
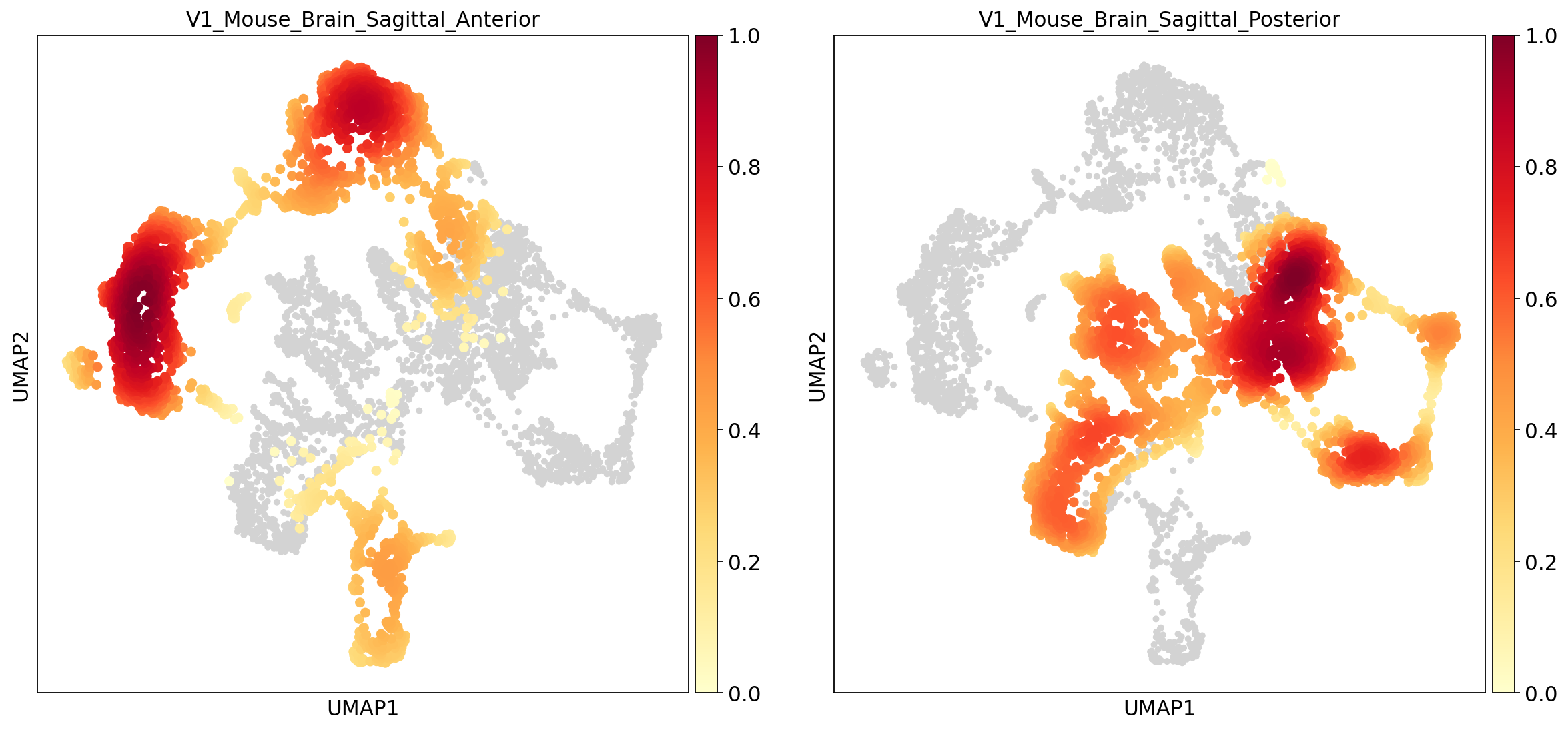
sc.pl.embedding_density(adata,groupby='batch')
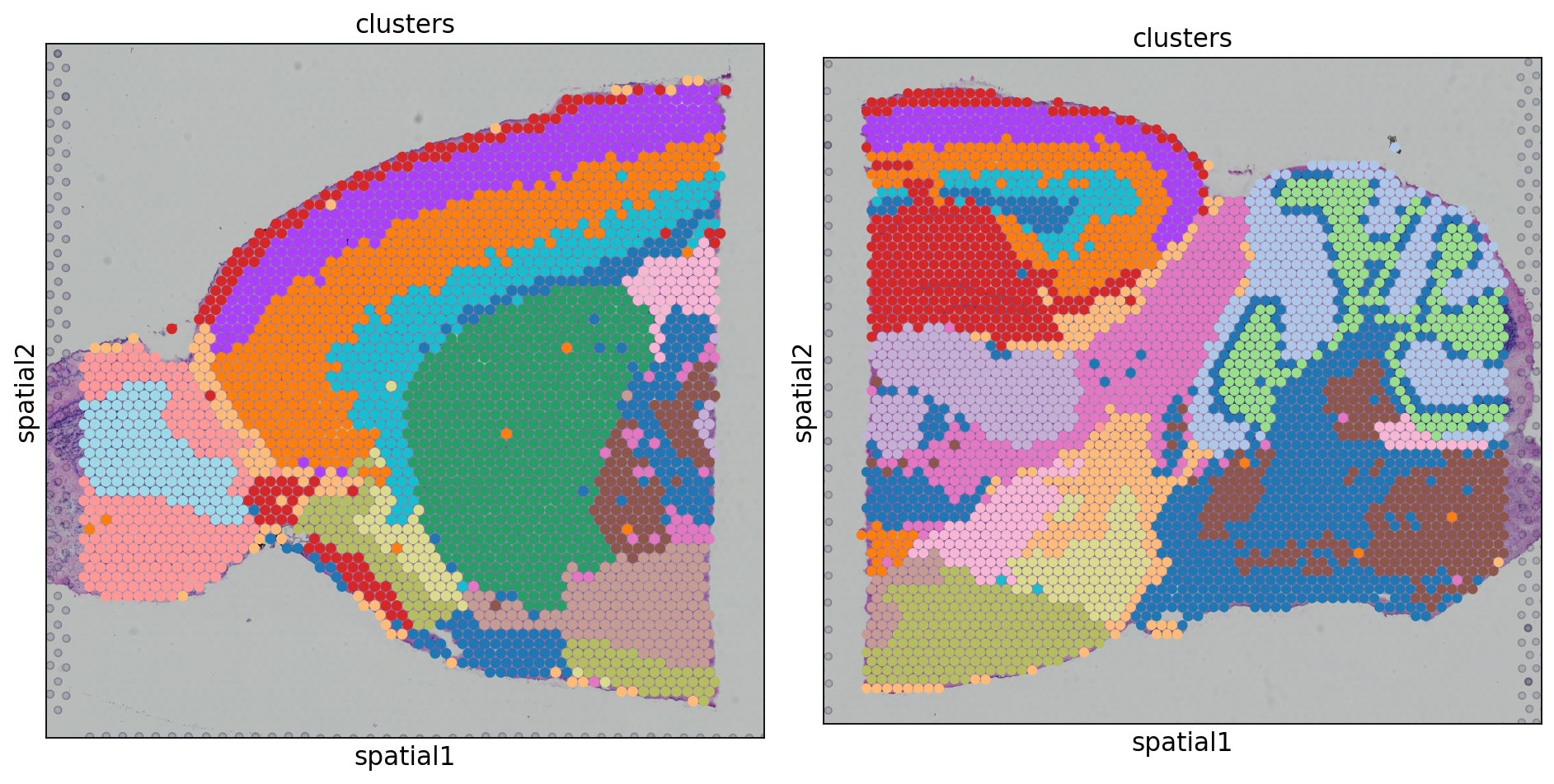
# spatial
clusters_colors = dict(
zip([str(i) for i in range(18)], adata.uns["clusters_colors"]))
fig, axs = plt.subplots(1, 2, figsize=(12, 8))
for i, batch in enumerate(
["V1_Mouse_Brain_Sagittal_Anterior", "V1_Mouse_Brain_Sagittal_Posterior"]
):
ad = adata[adata.obs.batch == batch, :].copy()
sc.pl.spatial(
ad,img_key="hires",
library_id = batch,
color="clusters",size=1.5,palette=[
v
for k, v in clusters_colors.items()
if k in ad.obs.clusters.unique().tolist()],
legend_loc=None,
show=False,
ax=axs[i], )
plt.tight_layout()
|
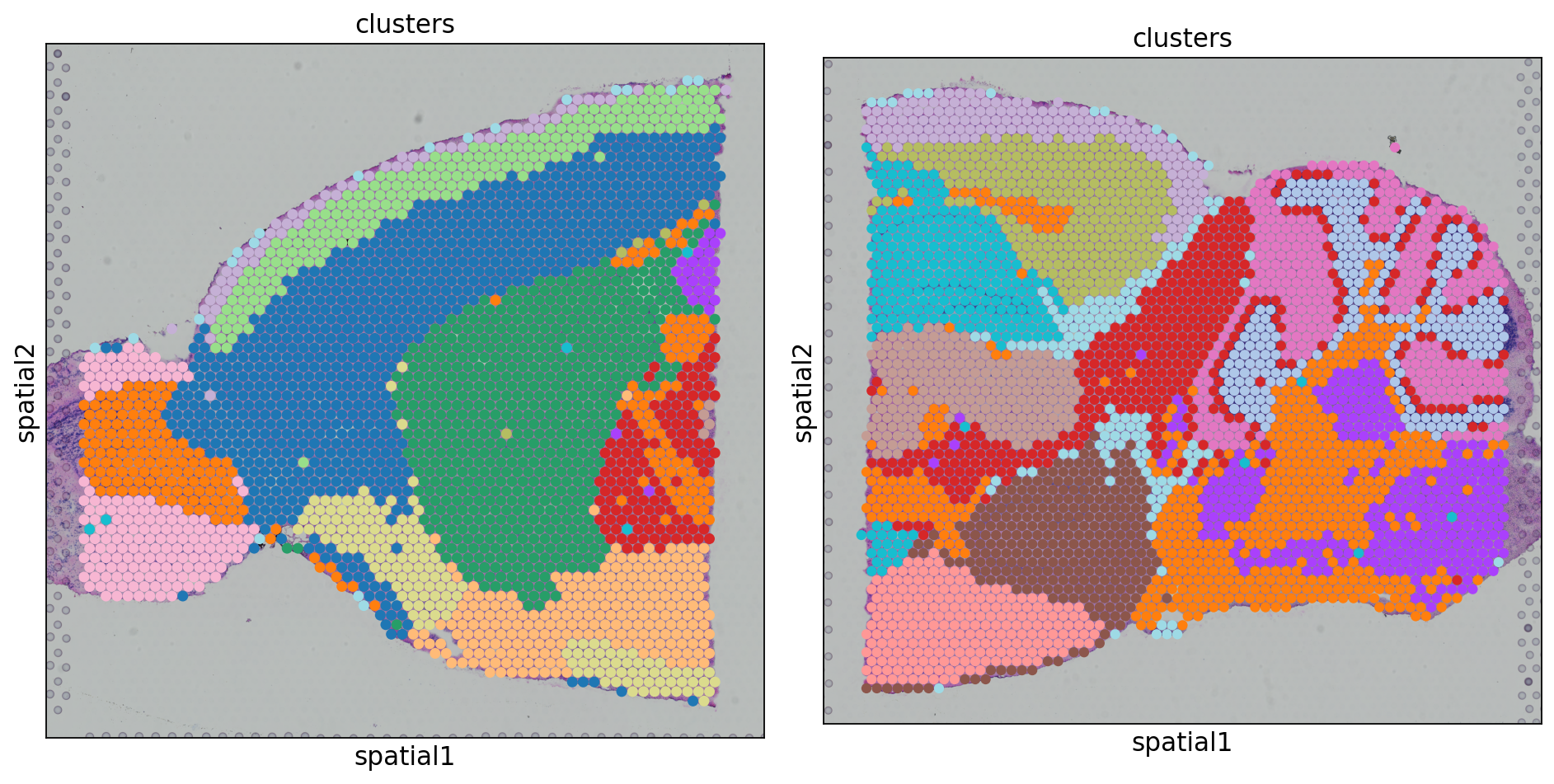
去批次操作
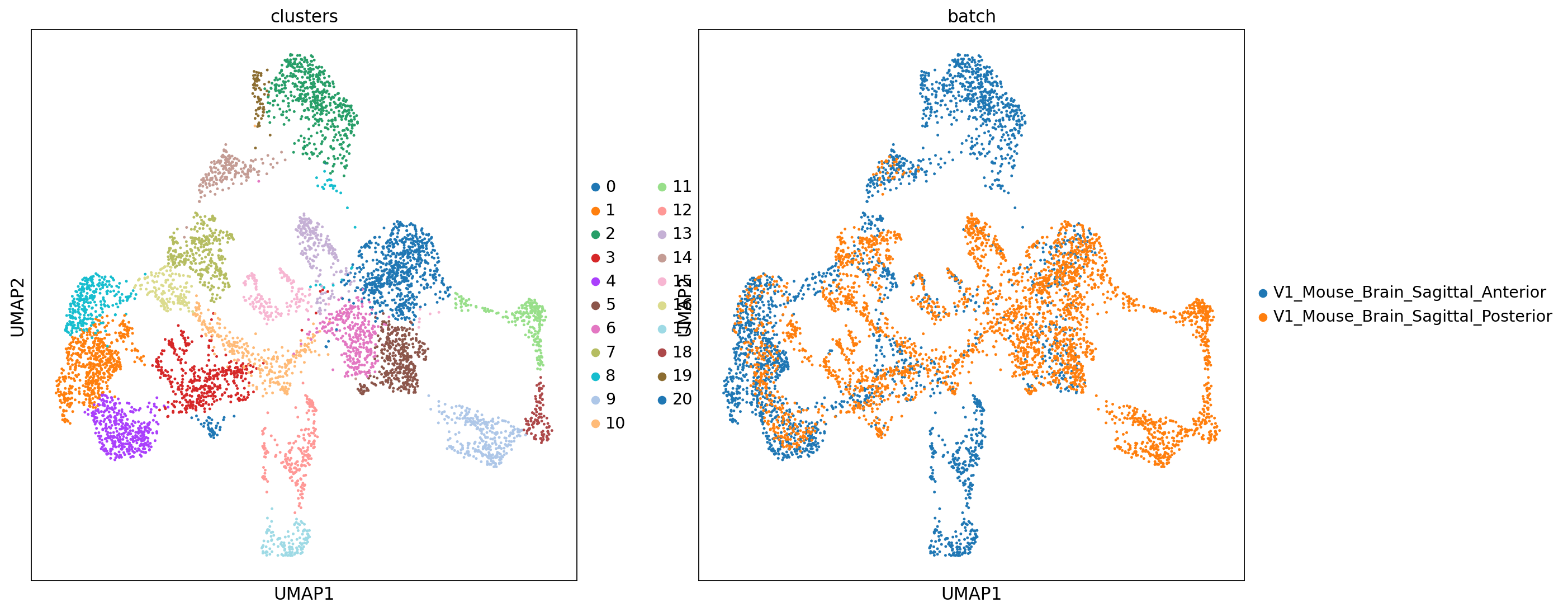
对于两张切片数据,我们的一个前提假设是二者至少有一定数量的相同的细胞类型(即细胞类型有一定的重合)。此时我们希望不同批次的相同细胞类型在umap图上相互靠近并聚为一类,而不是被聚为新的类。本例中在未经去批次处理的umap图上,batch0(蓝色)和batch1(橙色)似乎分的很开,二者只有少部分重合,而我们预期二者应当有较多的重合,这说明这二者之间存在这明显的批次效应。
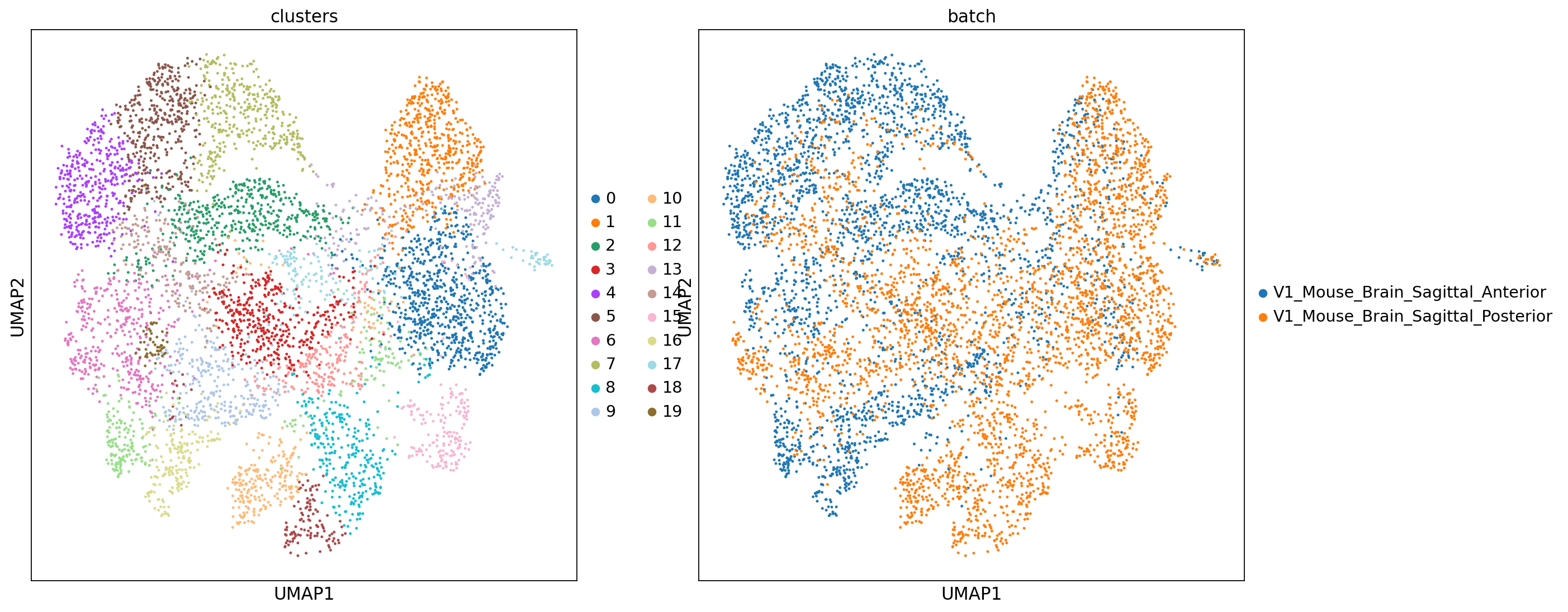
BBKNN去批次
1、安装BBKNN
1
2
|
# 安装BBKNN
pip install bbknn
|
2、去批次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
import bbknn
# 根据bbknn原理,该算法返回的是一个t-临近图,相当于是取代了原本的`sc.pp.neighbors(adata)`的作用。
# 当然,在此之前还是需要pca降维。
# 结果存储在`adata.uns['neighbors']`;`adata.obsp['distances']`和`adata['connectivities']`中。
bbknn.bbknn(adata)
# 根据bbknn生成的t临近图,重新计算umap图坐标、leiden聚类结果
sc.tl.umap(adata) #根据新的TNN结果计算umap图
sc.tl.leiden(adata,key_added='clusters',resolution=1) # 根据根据新的TNN结果进行leiden聚类
#### 可视化 ####
# umap
sc.pl.umap(adata,color=['clusters','batch'],palette=sc.pl.palettes.default_20)
# embedding_density
sc.tl.embedding_density(adata,groupby='batch')
sc.pl.embedding_density(adata,groupby='batch')
# spatial
clusters_colors = dict(
zip([str(i) for i in range(18)], adata.uns["clusters_colors"]))
fig, axs = plt.subplots(1, 2, figsize=(12, 8))
for i, batch in enumerate(
["V1_Mouse_Brain_Sagittal_Anterior", "V1_Mouse_Brain_Sagittal_Posterior"]
):
ad = adata[adata.obs.batch == batch, :].copy()
sc.pl.spatial(
ad,img_key="hires",
library_id = batch,
color="clusters",size=1.5,palette=[
v
for k, v in clusters_colors.items()
if k in ad.obs.clusters.unique().tolist()],
legend_loc=None,
show=False,
ax=axs[i], )
plt.tight_layout()
|
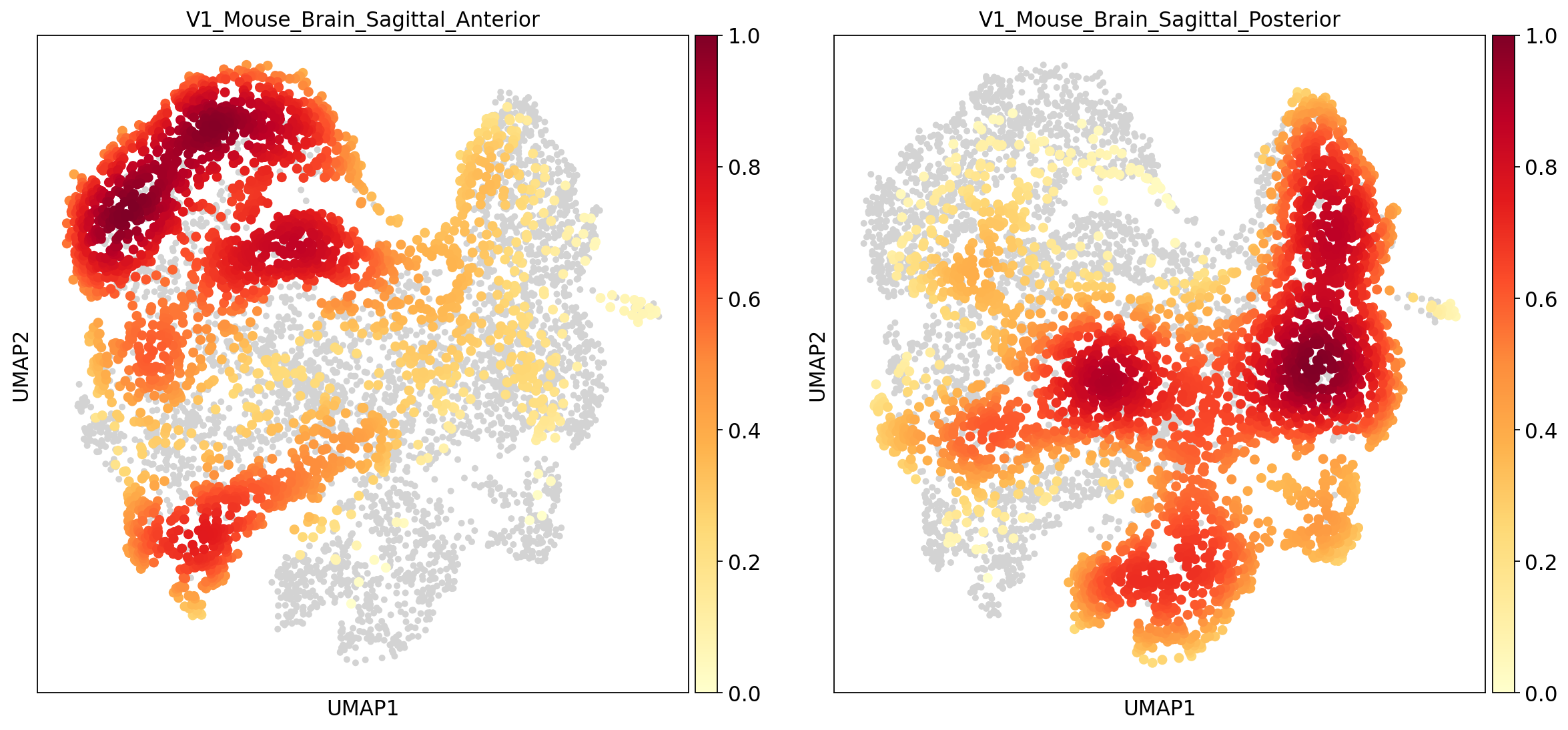
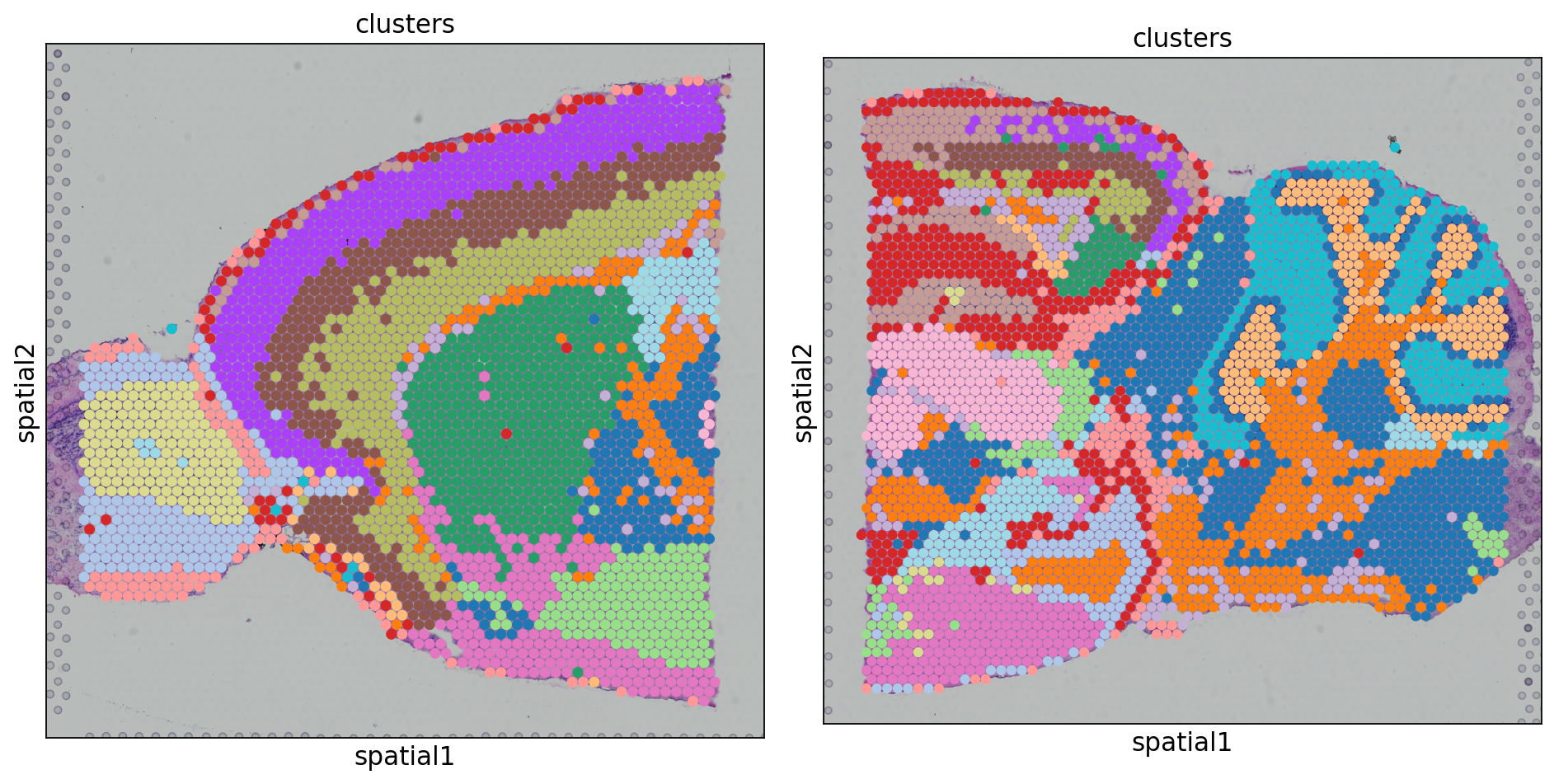
Combat去批次
Combat去批次的方式是直接对原始数据(adata.X)进行操作的。故这一步骤通常跟在标准化和取完对数之后:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
# 合并数据
adatas = [adata_spatial_anterior,adata_spatial_posterior]
adata = sc.concat(
adatas,label='batch',
uns_merge='unique',keys=[
k
for d in [
adatas[0].uns['spatial'],
adatas[1].uns['spatial'],
]
for k,v in d.items()
],
index_unique='-'
)
# 筛选高变基因
sc.pp.highly_variable_genes(adata, flavor='seurat', n_top_genes=2000)
# 备份原始数据,并取高变基因数据子集
adata.raw = adata
adata = adata[:, adata.var.highly_variable]
# 【关键步骤!】
sc.pp.combat(adata, key='batch')
# 后续降维与聚类
sc.pp.pca(adata, svd_solver='arpack')
sc.pp.neighbors(adata)
sc.tl.umap(adata)
sc.tl.leiden(adata, key_added='clusters', resolution=1)
#### 可视化 ####
# umap
sc.pl.umap(adata,color=['clusters','batch'],palette=sc.pl.palettes.default_20)
# embedding_density
sc.tl.embedding_density(adata,groupby='batch')
sc.pl.embedding_density(adata,groupby='batch')
# spatial
clusters_colors = dict(
zip([str(i) for i in range(18)], adata.uns["clusters_colors"]))
fig, axs = plt.subplots(1, 2, figsize=(12, 8))
for i, batch in enumerate(
["V1_Mouse_Brain_Sagittal_Anterior", "V1_Mouse_Brain_Sagittal_Posterior"]
):
ad = adata[adata.obs.batch == batch, :].copy()
sc.pl.spatial(
ad,img_key="hires",
library_id = batch,
color="clusters",size=1.5,palette=[
v
for k, v in clusters_colors.items()
if k in ad.obs.clusters.unique().tolist()],
legend_loc=None,
show=False,
ax=axs[i], )
plt.tight_layout()
|

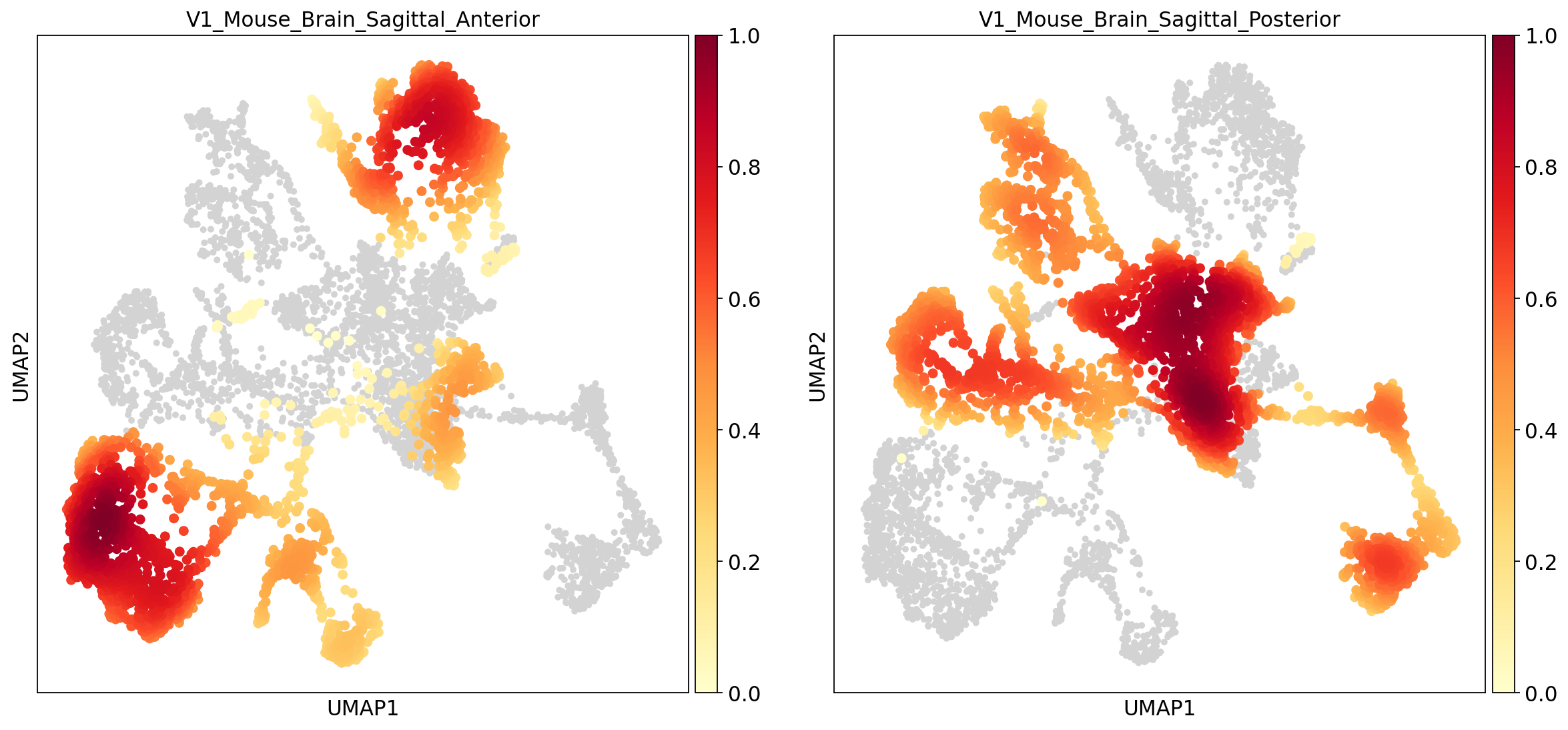
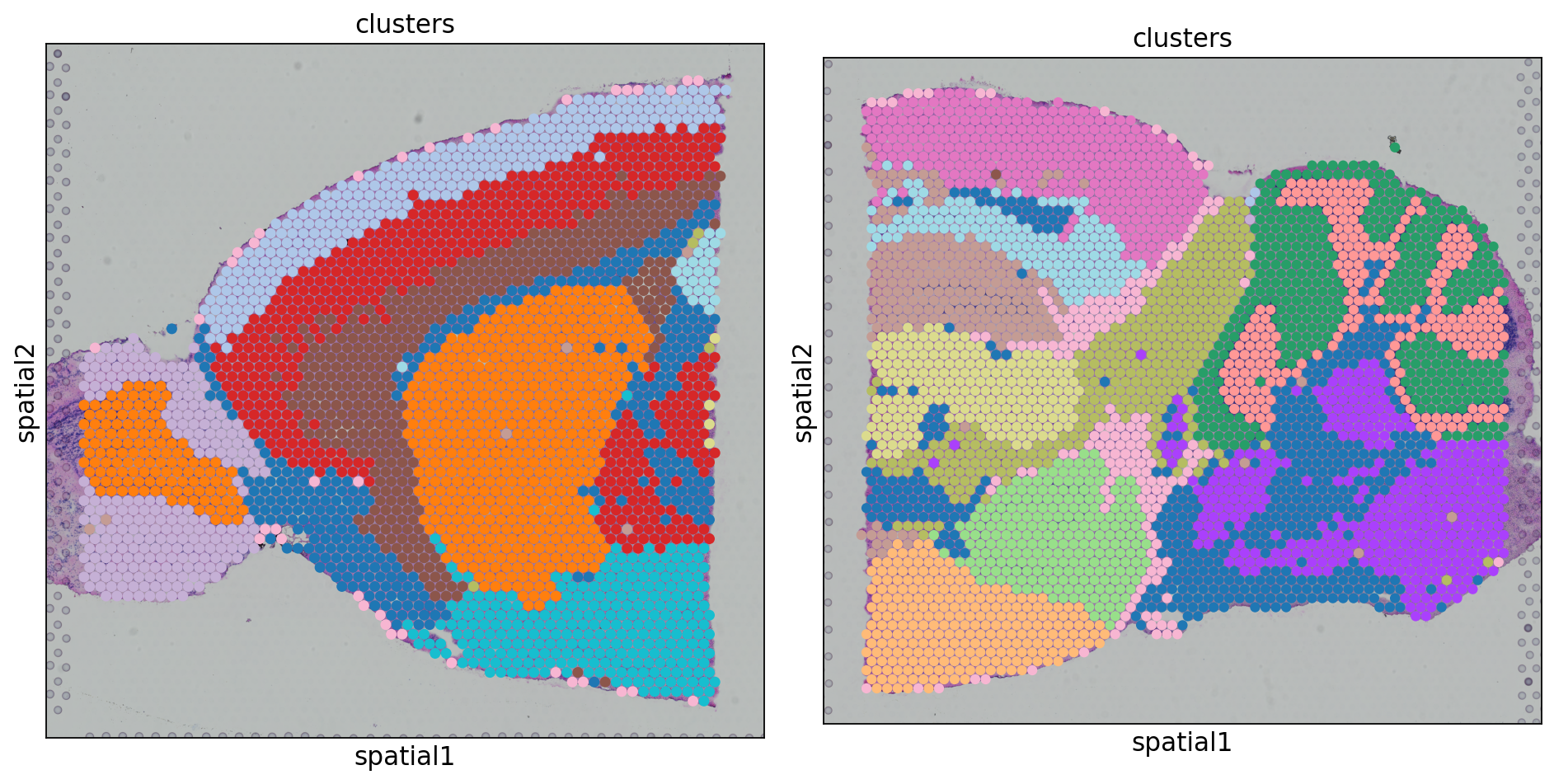
在该样本中combat表现非常不好,两个样本中的相同细胞类型并没有被聚类到一起。
harmony去批次
1、安装harmonypy
1
2
|
# 安装scanpy的扩展
pip install harmonypy
|
2、去批次
如上所述,harmony是针对主成分空间的坐标进行去批次的,因此最终输出的结果是修正过的主成分空间坐标,该坐标存储在adata.obsm[‘X_pca_harmony’]中。注意,原始的表达矩阵并没有被修改。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
adatas = [adata_spatial_anterior,adata_spatial_posterior]
adata = sc.concat(
adatas,label='batch',
uns_merge='unique',keys=[
k
for d in [
adatas[0].uns['spatial'],
adatas[1].uns['spatial'],
]
for k,v in d.items()
],
index_unique='-'
)
# 归一化,对数化筛选出高变基因
## sc.pp.normalize_total(adata,inplace=True)
## sc.pp.log1p(adata)
sc.pp.highly_variable_genes(adata,flavor='seurat',n_top_genes=2000)
# 备份,然后删去非高变基因
adata.raw = adata
adata = adata[:,adata.var.highly_variable]
sc.pp.pca(adata,svd_solver = 'arpack')
# 【关键步骤!】
# 使用sc.external.pp.harmony_integrate()进行去批次,指定批次信息字段为adata.obs['batch']
sc.external.pp.harmony_integrate(adata,key='batch')
sc.pp.neighbors(adata,use_rep='X_pca_harmony') # 以X_pca_harmony为依据计算KNN
sc.tl.umap(adata) #根据新的KNN结果计算umap图
sc.tl.leiden(adata,key_added='clusters',resolution=1) # 根据根据新的KNN结果进行leiden聚类
#### 可视化 ####
# umap
sc.pl.umap(adata,color=['clusters','batch'],palette=sc.pl.palettes.default_20)
# embedding_density
sc.tl.embedding_density(adata,groupby='batch')
sc.pl.embedding_density(adata,groupby='batch')
# spatial
clusters_colors = dict(
zip([str(i) for i in range(18)], adata.uns["clusters_colors"]))
fig, axs = plt.subplots(1, 2, figsize=(12, 8))
for i, batch in enumerate(
["V1_Mouse_Brain_Sagittal_Anterior", "V1_Mouse_Brain_Sagittal_Posterior"]
):
ad = adata[adata.obs.batch == batch, :].copy()
sc.pl.spatial(
ad,img_key="hires",
library_id = batch,
color="clusters",size=1.5,palette=[
v
for k, v in clusters_colors.items()
if k in ad.obs.clusters.unique().tolist()],
legend_loc=None,
show=False,
ax=axs[i], )
plt.tight_layout()
|
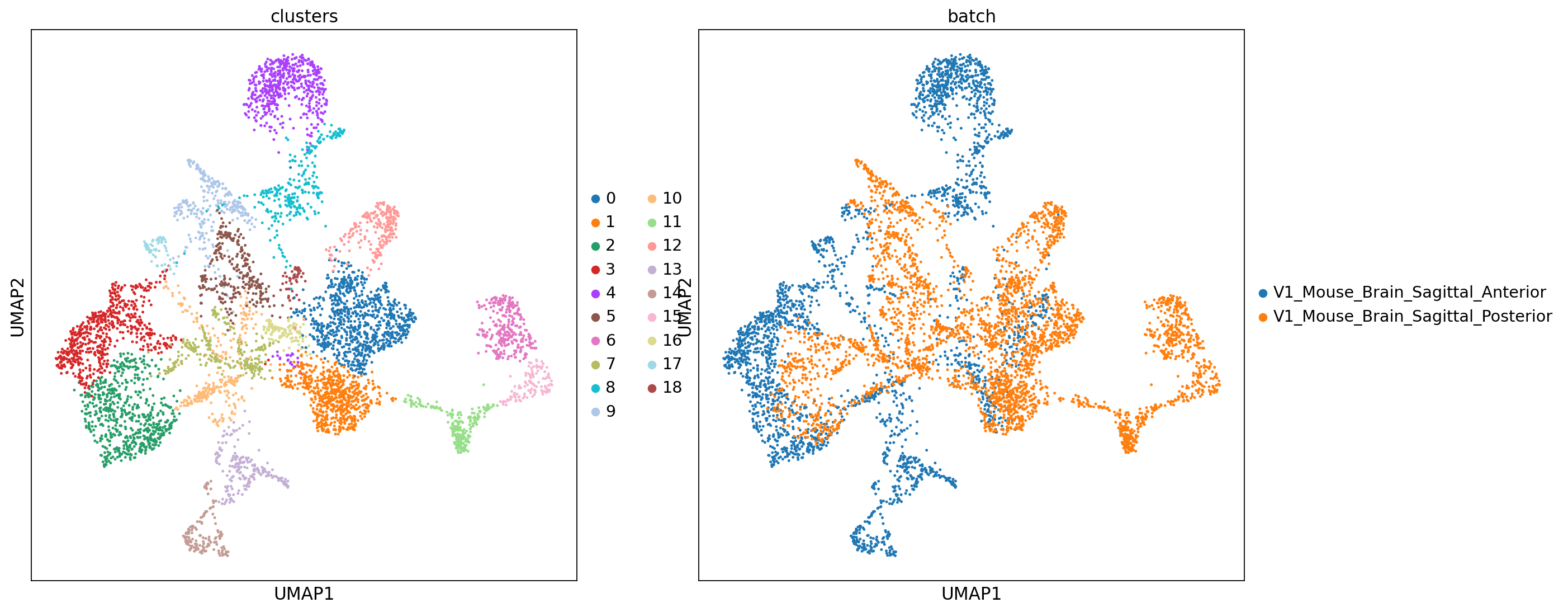
Scanorama去批次
Scanorama作用在数据合并的时候,通过传入adata列表,Scanorama可以对列表中的所有Anndata对象进行去批次操作,并且处理完毕的对象仍以列表的形式返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
# 【关键步骤!】将所有的空间转录结果构建列表,再运行scanorma进行矫正,对批次效应进行去除
# 与BBKNN一样,也是对PCA坐标进行操作。不过程序内部就会进行主成分分析,原先的sc.pp.pca()不是必要的
adata_spatial_anterior = sc.read('data/k8/adata_spatial_anterior.h5ad')
adata_spatial_posterior = sc.read('data/k8/adata_spatial_posterior.h5ad')
# 使基因名唯一
adata_spatial_anterior.var_names_make_unique()
adata_spatial_posterior.var_names_make_unique()
###### 首先分别进行标准化与取对数?
sc.pp.normalize_total(adata_spatial_anterior,inplace=True)
sc.pp.log1p(adata_spatial_anterior)
sc.pp.normalize_total(adata_spatial_posterior,inplace=True)
sc.pp.log1p(adata_spatial_posterior)
adatas = [adata_spatial_anterior,adata_spatial_posterior,]
adatas_cor = scanorama.correct_scanpy(adatas,return_dimred=True)
# 将两个数据进行合并
adata = sc.concat(
adatas_cor,label='batch',
uns_merge='unique',keys=[
k
for d in [
adatas_cor[0].uns['spatial'],
adatas_cor[1].uns['spatial'],
]
for k,v in d.items()
],
index_unique='-'
)
# 降维聚类
sc.pp.neighbors(adata,use_rep='X_scanorama')
sc.tl.umap(adata)
sc.tl.leiden(adata,key_added='clusters',resolution = 0.6)
# 可视化
sc.pl.umap(adata,color=['clusters','batch'],palette=sc.pl.palettes.default_20)
sc.tl.embedding_density(adata,groupby='batch')
sc.pl.embedding_density(adata,groupby='batch')
# 最终在切片图片上标注上对应的细胞类型。想要达到的效果即不同切片上的相同细胞类型的颜色需要一致
clusters_colors = dict(
zip([str(i) for i in range(18)], adata.uns["clusters_colors"]))
fig, axs = plt.subplots(1, 2, figsize=(12,8))
for i, batch in enumerate(
["V1_Mouse_Brain_Sagittal_Anterior", "V1_Mouse_Brain_Sagittal_Posterior"]
):
ad = adata[adata.obs.batch == batch, :].copy()
sc.pl.spatial(
ad,img_key="hires",
library_id = batch,
color="clusters",size=1.5,palette=[
v
for k, v in clusters_colors.items()
if k in ad.obs.clusters.unique().tolist()],
legend_loc=None,
show=False,
ax=axs[i], )
plt.tight_layout()
|
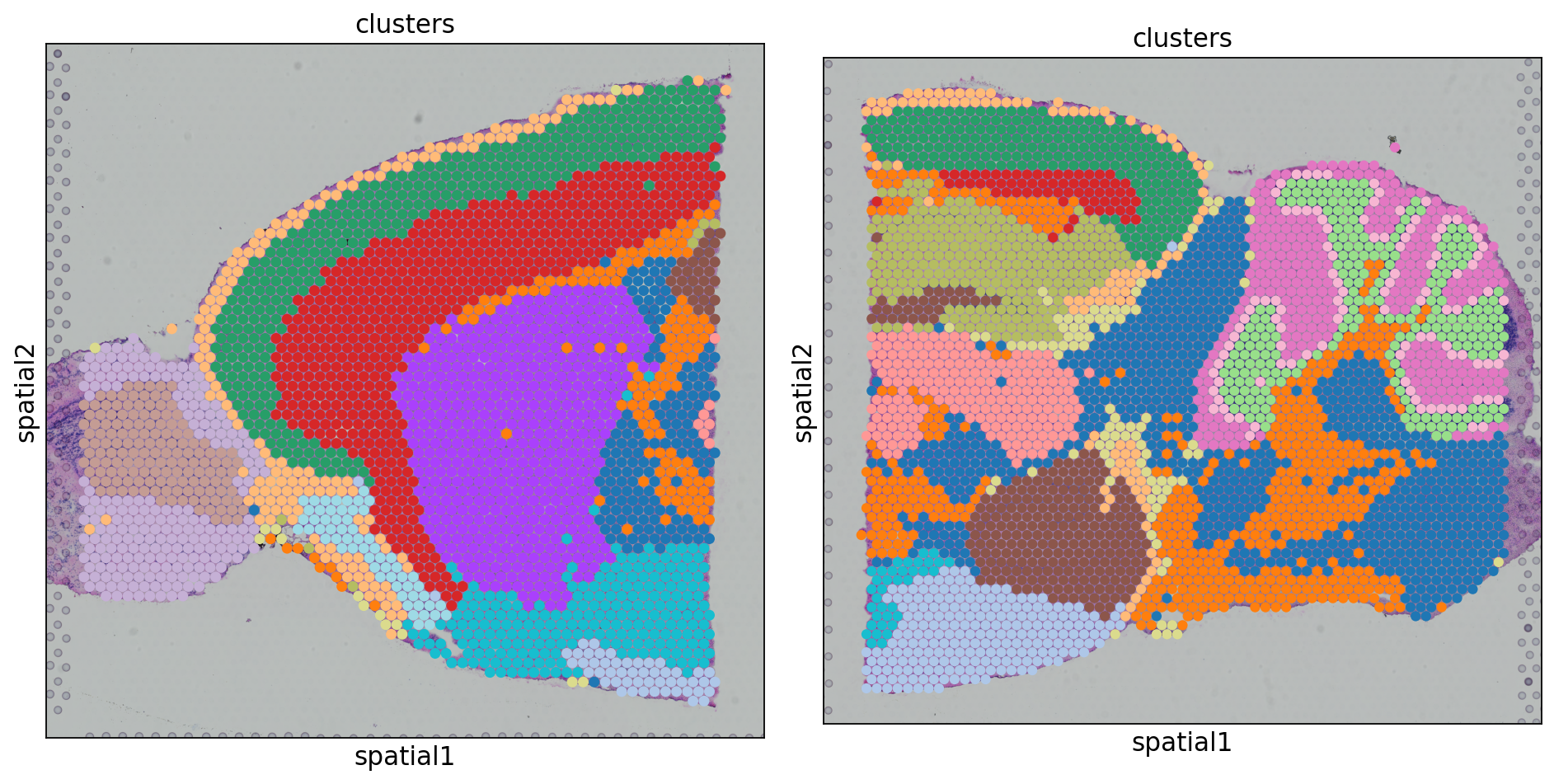
几种工具的比较
|
输入 |
输出 |
特点 |
| BBKNN |
PCA坐标 |
t-临近图 |
快速,非线性对齐 |
| Combat |
表达矩阵 |
表达矩阵 |
不能处理复杂非线性批次偏差 |
| Harmony |
PCA坐标 |
PCA坐标 |
适用于复杂数据集;可以保持生物学信号 |
| Scanorama |
PCA坐标 |
PCA坐标 |
非监督整合,多数据集拼接能力强 |
总之,对于拥有相同细胞类型的不同批次数据,可以使用BBKNN算法;如果要使用原始的表达矩阵进行下游分析,可以使用Combat;如果每个批次细胞类型不完全相同,可以使用Harmony;如果存在很多个批次,可以使用Scanorama。对于本例来说Harmony的表现效果最佳,可以作为首选。最终选取哪个去批次方法还需要在后面进行进一步验证。




