基于QIIME2的16SrRNA测序分析

QIIME2使用-16S扩增子测序分析

最初的准备

16SRNA的结构

16SRNA基因全长1500bp左右，基因序列包括间隔分布的保守区和可变区，对于细菌一般包括9个保守区（C1-C9）和9个可变区（V1-V9）。不同种类的细菌有相同的保守区序列和不同的可变区序列，因此可以根据保守区序列设计引物来扩增环境样品中所有细菌16SrRNA基因，而根据可变区序列来区分不同种类的细菌。

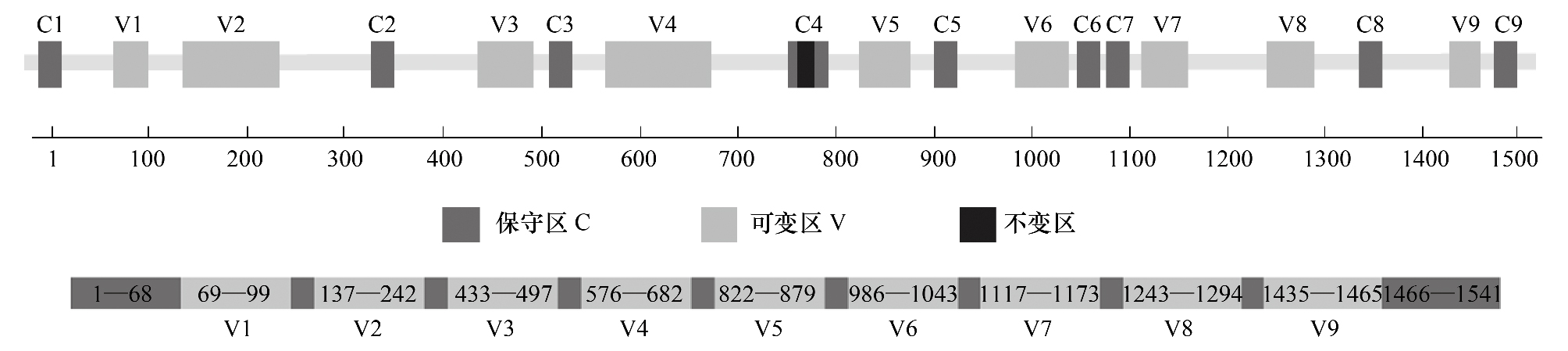16S rRNA基因在微生物生态学中的应用传统方法中最常用的引物是27F和1492R，几乎能扩增出完整的16SrRNA基因全长。而由于二代高通量测序平台读长的限制，只能对16SrDNA的某一段可变区进行测序。有的文献中选择测单V区（V3/V4/V6），有的测双V区（V3-V4区或V4-V5区），还有的选择三V区（V1-V3区、V5-V7区或V7-V9区)进行16S rDNA测序。一般而言，环境微生物组学常用的测序区域是V3-V4，V4-V5，或者单测V4区。在Illumina时代，由于平台测序长度的限制，V4单区测序（515F/806R)被更为广泛地使用。也是[地球微生物计划](16S Illumina Amplicon Protocol : earthmicrobiome)中推荐使用的引物序列。

而在2016年，Walters et al.对测序引物进行了改造，对一些简并引物进行了改进。相比之前，不仅对细菌群落的检测进行了矫正，还可以多测出来许多古菌。因此对于环境样本而言，使用改进后的515F/806R or 515F/926R，可能在行业标准日益规范的今天，是一个更好地选择，今后应该会成为16S检测微生物多样性测序的首选。

Primer Name	Primer Sequence	Author
515F Original	GTGCCAGCMGCCGCGGTAA	Coporaso et al.
806R Original	GGACTACHVGGGTWTCTAAT	Coporaso et al.
515F Modified	GTGYCAGCMGCCGCGGTAA	Parada et al.
806R Modified	GGACTACNVGGGTWTCTAAT	Apprill et al.
926R	CCGYCAATTYMTTTRAGTTT	Parada et al.

示例数据的下载

在本教程中，你将使用 QIIME 2 对来自两个个体的四个身体部位在五个时间点的人体微生物组样本进行分析，其中第一个时间点紧接在抗生素使用之后。数据是通过 Illumina HiSeq 测序平台，采用地球微生物组计划（Earth Microbiome Project）的高变区 4（V4）16S rRNA 测序协议进行测序的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


####教程文件的下载####
# 新建文件夹
mkdir QIIME2_04
cd QIIME2_04

# 元数据metadata的下载
wget \
  -O "sample-metadata.tsv" \
  "https://data.qiime2.org/2024.10/tutorials/moving-pictures/sample_metadata.tsv"

# 测序数据的下载。这里只用了原始测序数据的一个子集，以提高运行速度。
mkdir -p emp-single-end-sequences
wget \
  -O "emp-single-end-sequences/barcodes.fastq.gz" \
  "https://data.qiime2.org/2024.10/tutorials/moving-pictures/emp-single-end-sequences/barcodes.fastq.gz"
# 
wget \
  -O "emp-single-end-sequences/sequences.fastq.gz" \
  "https://data.qiime2.org/2024.10/tutorials/moving-pictures/emp-single-end-sequences/sequences.fastq.gz"

以下是刚才下载的几个文件的结构：

1、sample-metadata.tsv，包括了实验每个样本的编号、测序barcode以及其它采样时的数据。

2、emp-single-end-sequences/barcodes.fastq，包含了每个测序reads的barcode序列，相当于将原始reads中的barcode区域单独拆分开。

3、emp-single-end-sequences/sequences.fastq，包含了Illumina测序中去除了barcodes的reads。每一个条目和上一个文件是一一对应的。

生成QIIME2对象

用于输入到QIIME 2的所有数据都以QIIME 2对象的形式出现，其中包含有关数据类型和数据源的信息。因此，我们需要做的第一件事是将这些序列数据文件导入到QIIME 2对象中。

这个QIIME 2对象的语义类型是EMPSingleEndSequences。QIIME 对象EMPSingleEndSequences是包含多样本混合的序列文件，这意味着序列尚未分配给样本（因此包括sequences.fastq.gz和barcode.fastq.gz文件，其中barcode.fastq.gz包含与sequences.fastq.gz中的每个序列相关联的条形码）。

指定存放两个fastq格式文件的文件夹，并将其打包生成EMPSingleEndSequences对象：

1
2
3
4


time qiime tools import \
  --type EMPSingleEndSequences \
  --input-path emp-single-end-sequences \
  --output-path emp-single-end-sequences.qza

拆分样品

根据提供的metadata，将测序结果分配到每一个样本。

运行以下命令来对序列进行样本拆分。demux emp-single命令指的是这些序列是根据地球微生物组计划标准方法添加的条形码，并且是单端序列。QIIME 2对象demux.qza包含样本拆分后的序列。第二个输出文件 (demux-details.qza) 包括Golay标签错误校正的详细。

1
2
3
4
5
6
7
8
9


time qiime demux emp-single \
  --i-seqs emp-single-end-sequences.qza \
  --m-barcodes-file sample-metadata.tsv \
  --m-barcodes-column barcode-sequence \
  --o-per-sample-sequences demux.qza \
  --o-error-correction-details demux-details.qza
  
# demux即demultiplex，拆分
# 指定上一步生成的混合样本的qza文件、指定metadata、输出文件名等。

拆分后的结果统计

样本拆分之后，生成拆分结果的统计信息非常重要。这允许我们确定每个样本获得多少序列，并且还可以获得序列数据中每个位置处序列质量分布的摘要。对于生成的qzv可视化对象，可以用网页来打开。该文件由三部分构成：一个不同数据量分布频率柱状图、一个每个样本的测序量以及一个交互式质量图。

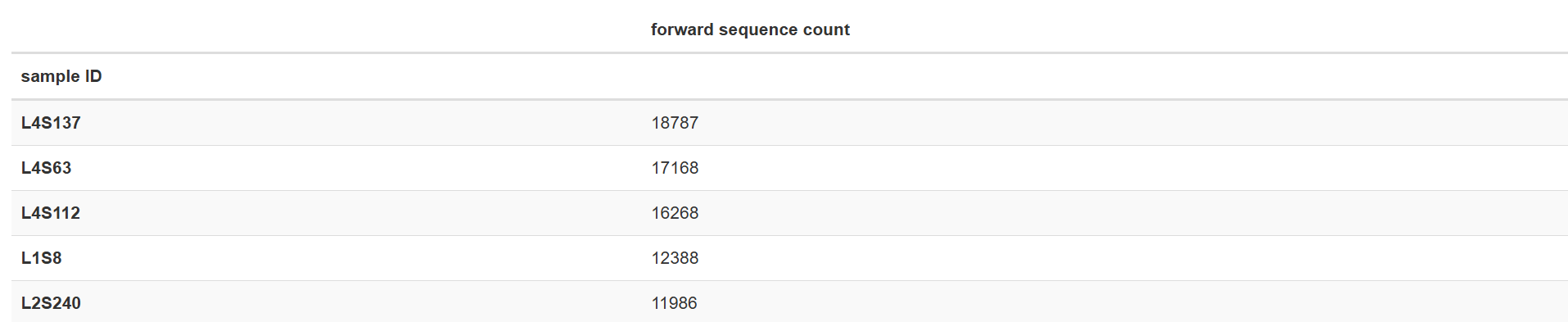
1
2
3


time qiime demux summarize \
  --i-data demux.qza \
  --o-visualization demux.qzv

序列质控和生成特征表

DADA2是用于检测和校正Illumina扩增序列数据的工作流程。正如在q2-dada2插件中实现的，这个质量控制过程将过滤掉在测序数据中鉴定的任何phiX序列（通常存在于标记基因Illumina测序数据中，用于提高扩增子测序质量），并同时过滤嵌合序列。

dada2 denoise-single方法需要两个用于质量过滤的参数：--p-trim-left m，它去除每个序列的前m个碱基(如引物、标签序列barcode)；--p-trunc-len n，它在位置n截断每个序列，即去除右端低质量序列。这允许用户去除序列的低质量区域、引物或标签序列等。为了确定要为这两个参数传递什么值，应该查看上面由qiime demux summarize生成的demux.qzv文件中的交互质量图选项卡。这里--p-trim-left选择0，--p-trunc-len选择120。

该命令生成三个输出文件：stats-dada2.qza: dada2计算统计结果，table-dada2.qza: 特征表，rep-seqs-dada2.qza: 代表序列。stats-dada2.qza内容为每个样本的输入、过滤、去噪和非嵌合的统计，并支持按列排序，检索和功能，用于样本异常筛选，特征表抽平标准化非常有用。

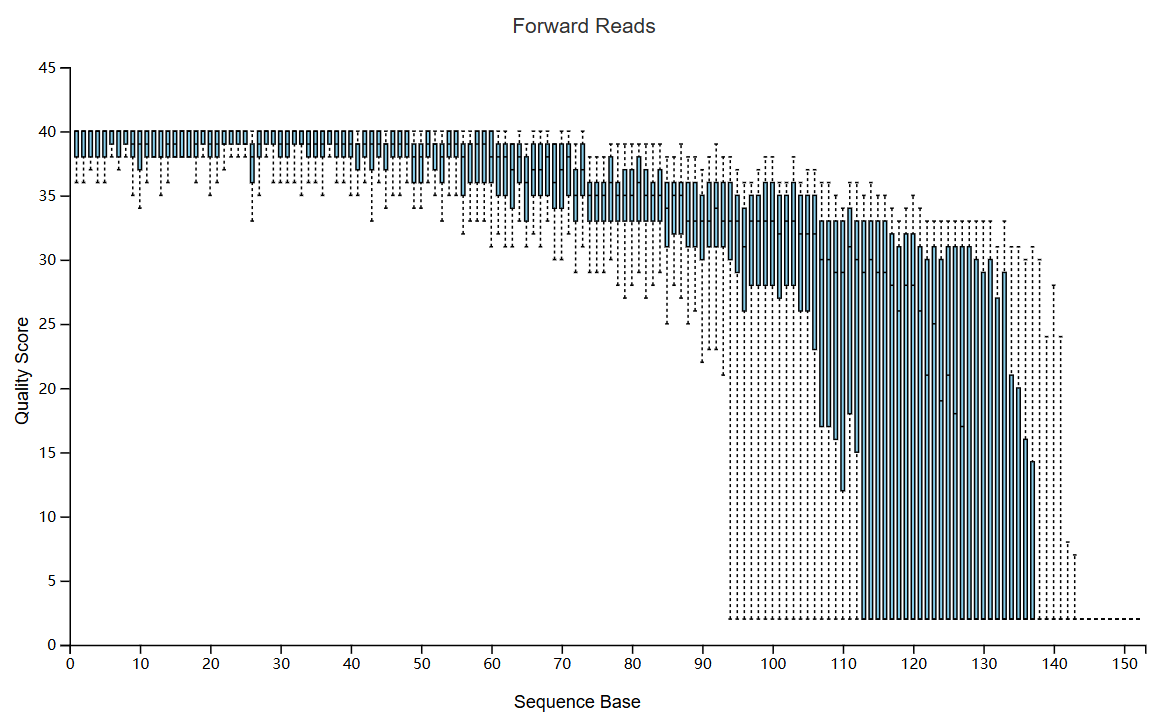
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


time qiime dada2 denoise-single \
  --i-demultiplexed-seqs demux.qza \
  --p-trim-left 0 \
  --p-trunc-len 120 \
  --o-representative-sequences rep-seqs-dada2.qza \
  --o-table table-dada2.qza \
  --o-denoising-stats stats-dada2.qza

# 对生成的三个文件分别可视化
qiime metadata tabulate \
  --m-input-file stats-dada2.qza \
  --o-visualization stats-dada2.qzv
  
qiime metadata tabulate \
  --m-input-file table-dada2.qza \
  --o-visualization table-dada2.qzv

qiime metadata tabulate \
  --m-input-file rep-seqs-dada2.qza \
  --o-visualization rep-seqs-dada2.qzv
  
# 改名，方便下一步分析
mv rep-seqs-dada2.qza rep-seqs.qza
mv table-dada2.qza table.qza

1、stats-dada2.qzv记录了每个样本的质控情况

2、table-dada2.qzv记录了每个样本的每个特征的出现频率。这里的特征即修剪后的120bp的reads，这里经过了MD5处理。

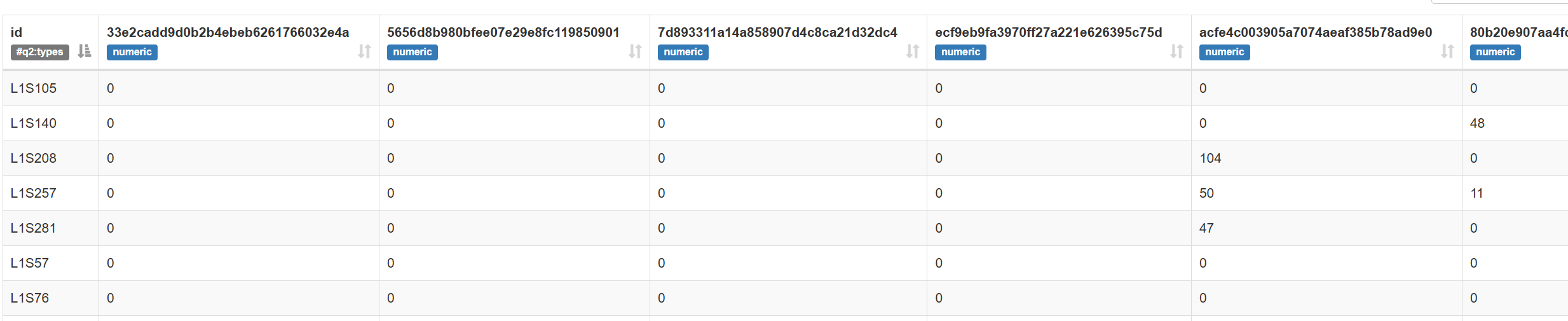
3、rep-seqs-dada2.qzv提供了序列与其MD5值的一一对应关系。

特征表和特征序列汇总

特性表汇总命令（feature-table summarize）将向你提供关于与每个样品和每个特性相关联的序列数量、这些分布的直方图以及一些相关的汇总统计数据的信息。特征表序列表格feature-table tabulate-seqs命令将提供特征ID到序列的映射，并提供链接以针对NCBI nt数据库轻松BLAST每个序列。当你想要了解关于数据集中重要特性的更多信息时，可视化将在本教程的后续分析中非常有用。

1
2
3
4
5
6
7
8


qiime feature-table summarize \
  --i-table table.qza \
  --o-visualization table.qzv \
  --m-sample-metadata-file sample-metadata.tsv

qiime feature-table tabulate-seqs \
  --i-data rep-seqs.qza \
  --o-visualization rep-seqs.qzv

1、table.qzv，与table-dada2.qzv类似，不过额外提供给了metadata数据，方便进一步可视化。

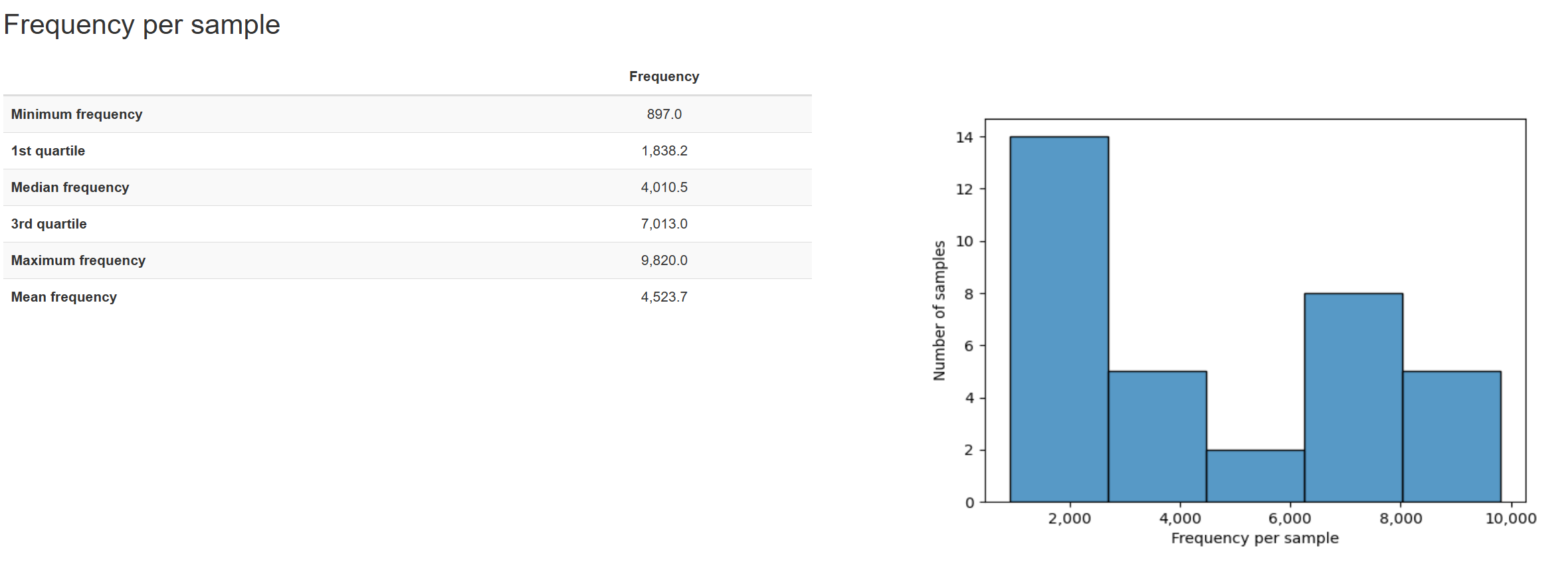
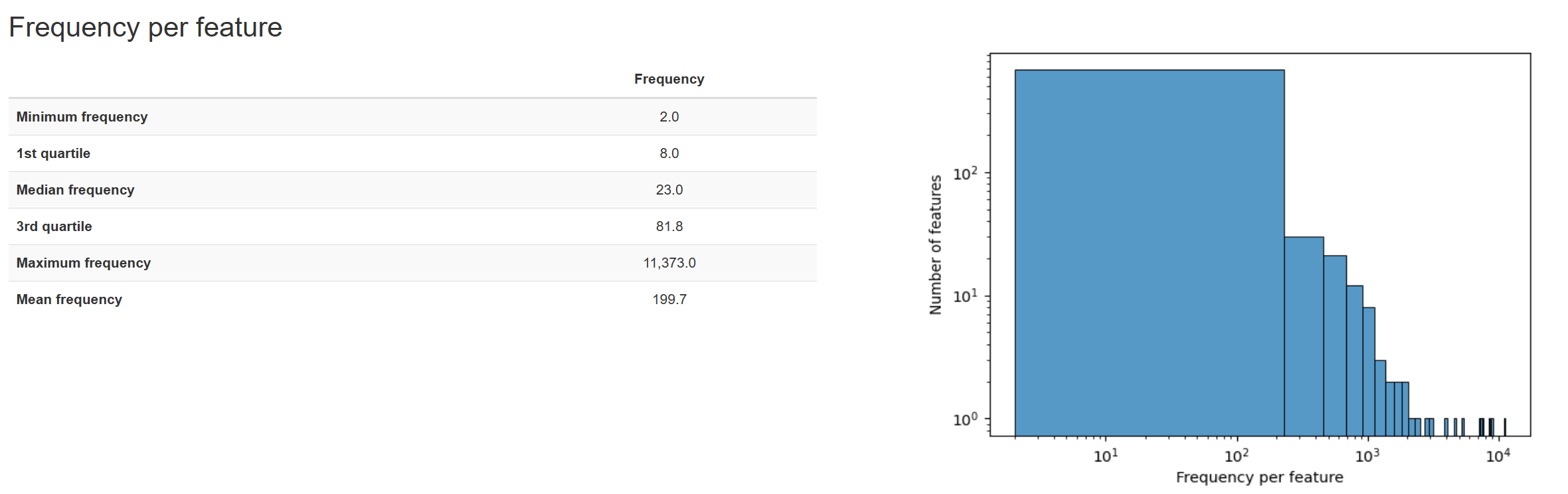
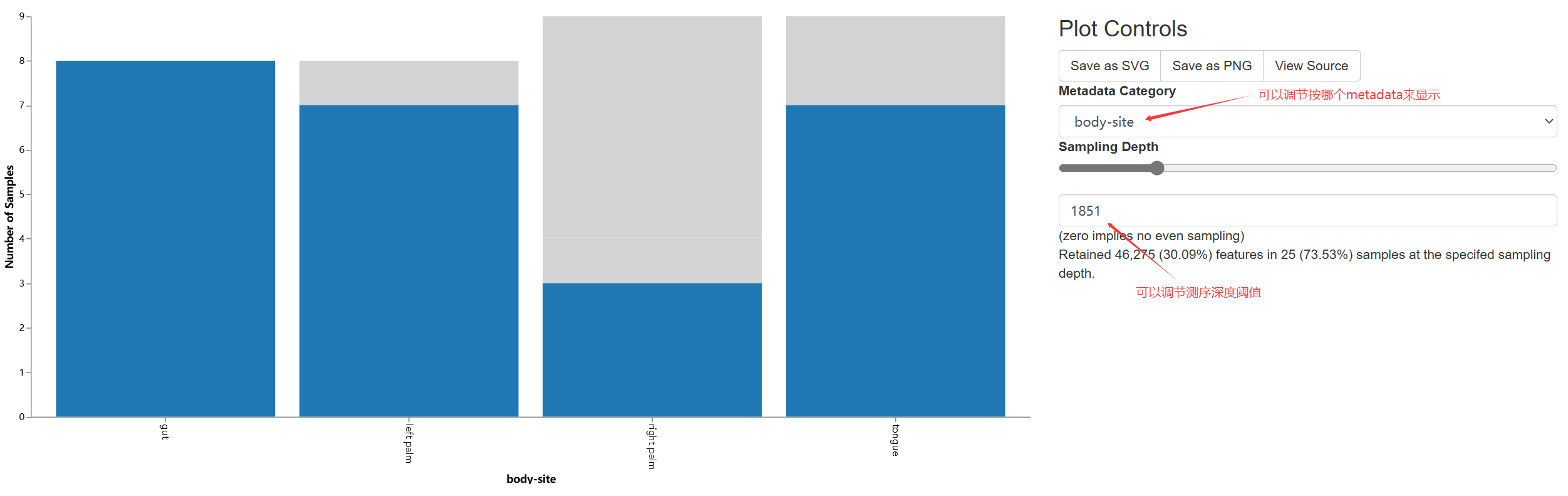
2、rep-seqs.qzv也与rep-seqs-dada2.qzv类似。

构建进化树用于多样性分析

序列对齐与进化树的构建

双序列比对是指对两条序列进行比对，找到其相似性关系，这种寻找生物序列相似性关系的过程被称为双序列比对。其算法可以主要分成基于全局比对的Needleman-Wunsch算法和基于局部比对的Smith-Waterman局部比对算法（均为动态规划算法）。多序列比对是双序列比对推广，即把两个以上字符序列对齐，逐列比较其字符的异同，使得每一列字符尽可能一致，以发现其共同的结构特征的方法称为多序列比对。对比后通过比较两两间的差异性（如编辑距离），可用于通过构建系统发育树（Phylogenetic tree）来帮助建立进化关系。构建的进化树的信息在后面计算α和β多样性的时候会用到。

代码实现

QIIME 2支持几种系统发育多样性度量方法，包括Faith’s Phylogenetic Diversity、weighted和unweighted UniFrac。除了每个样本的特征计数（即QIIME2对象FeatureTable[Frequency]）之外，这些度量还需要将特征彼此关联结合有根进化树。此信息将存储在一个QIIME 2对象的有根系统发育对象Phylogeny[Rooted]中。为了生成系统发育树，我们将使用q2-phylogeny插件中的align-to-tree-mafft-fasttree工作流程。

首先，工作流程使用mafft程序执行对FeatureData[Sequence]中的序列进行多序列比对，以创建QIIME 2对象FeatureData[AlignedSequence]。接下来，流程屏蔽（mask或过滤）对齐的的高度可变区(高变区)，这些位置通常被认为会增加系统发育树的噪声。随后，流程应用FastTree基于过滤后的比对结果生成系统发育树。FastTree程序创建的是一个无根树，因此在本节的最后一步中，应用根中点法将树的根放置在无根树中最长端到端距离的中点，从而形成有根树。

输出结果文件:aligned-rep-seqs.qza: 多序列比对结果，masked-aligned-rep-seqs.qza: 过滤去除高变区后的多序列比对结果，rooted-tree.qza: 有根树，用于多样性分析，unrooted-tree.qza: 无根树。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


time qiime phylogeny align-to-tree-mafft-fasttree \
  --i-sequences rep-seqs.qza \
  --o-alignment aligned-rep-seqs.qza \
  --o-masked-alignment masked-aligned-rep-seqs.qza \
  --o-tree unrooted-tree.qza \
  --o-rooted-tree rooted-tree.qza

#### 分别进行可视化

# 可视化多序列对比结果
qiime feature-table tabulate-seqs \
  --i-data aligned-rep-seqs.qza \
  --o-visualization aligned-rep-seqs.qzv
  
# 可视化过滤去除高变区后的多序列对比结果（高变区可能是由于测序错误，而保守区的改变可能提示新的物种）
qiime feature-table tabulate-seqs \
  --i-data masked-aligned-rep-seqs.qza \
  --o-visualization masked-aligned-rep-seqs.qzv
  
# 有根树和无根树无法可视化，但是可以用以下命令导出为tree.nwk文件，然后在https://itol.embl.de网站上可视化
qiime tools export \
  --input-path unrooted-tree.qza \
  --output-path exported-tree
  
qiime tools export \
  --input-path rooted-tree.qza \
  --output-path exported-tree

多重序列对比结果

系统发育树，可以看到每个序列之间的亲缘关系。每个节点的名称是原始序列的MD5值。

α多样性分析和β多样性分析

α与γ多样性

α 多样性指数是用于测量群落内生物种类数量以及生物种类间相对多度的一种测量。而γ多样性则类似于把各个群落综合起来看作一个整体来算总的α多样性。它们反映了群落内物种间通过竞争资源或利用同种生境而产生的共存结果，可分为:

物种丰富度指数

反映了一定空间范围内生物的丰富程度。最古老、最简单的方式是以某空间中的物种数来表示。另外，应用广泛的还有Margalef 丰富度指数、Menhnick 丰富度指数等，这些指数分别可以用物种数目与样方面积的大小或个体总数的不同数学关系来测量。使用丰富度指数需要注意的是，不同的植物群落，丰富度指数的适用情况不同，要选择相对稳定的指数。另外，丰富度指数的大小受样地面积的影响较大，而且忽略了富集种和稀疏种对于群落多样性贡献的不同。因此，在应用丰富度指数时必须与均匀度指数等结合起来，才能更客观地反映群落的多样性水平。如下图，地点A比地点B拥有更多的物种，但是由于各物种丰度十分不均匀，物种丰富度指数不能完全反应真实情况。

$$ Gleason\ index:\ D = \frac{S}{lnA}\\ $$ $$ Margalef\ index:\ D=\frac{S-1}{lnN} $$

前者中S为群落中物种数目，A为调查的总面积；后者中S为群落中的物种总数目，N为观察到的所有物种的个体总数。

物种均匀度指数

均匀度指数是用来刻画群落中各个种的相对密度，有Pielou 均匀度指数，Sheldon 均匀度指数，Hill 均匀度指数、Heip 均匀度指数、Alatalo均匀度指数等，这些指数与丰富度指数呈正相关。

$$ Pielou\ index:\ E=\frac{H}{lnS} $$

其中H是香农指数（见下文），S为物种数。

物种多样性指数

物种多样性指数是将物种多样性和种的多度结合起来的函数，最常用的有Shannon—Wienner 多样性指数，Simpson 多样性指数，Hill 多样性指数以及种间相遇概率（PIE）等。其中，Simpson 指数反映的是优势种在群落中的地位和作用，也成为生态优势度，它与其他多样性指数均呈负相关。多样性指数越高，生态优势度越小，而均匀度指数越高。

$$ Shannon-wiener\ index:\ H=-\sum_i{P_i\ln{P_i}}，\ H_{max}=lnS\\ Simpson\ index:\ D=\sum_i{P_i^{2}}\\ Gini-Simpson\ index:\ D=1-\sum_i{P_i^{2}} $$

式中Ni为种i的个体数，N为所在群落的所有物种的个体数之和。S为物种数，Pi指第i种的个体数占群落中总个体数的比例。

然而，在现代，我们要求生物多样性估计量需符合“倍增原则”，即将N个物种丰富度结构相同，且组成物种完全不同的群集等权数混合，其生物多样性会是单一群集的N倍。有鉴于此，Jost (2006)认为应该要使用有效物种数的概念来表达多样性，才能符合倍增原则。有效物种数的概念，首先由 MacArthur (1965) 提出。群集的有效物种数，等同于与其拥有相同物种多样性水平的均匀分布的群集的物种数。Jost (2006) 认为有效物种数才是群集真正的多样性（This is the true diversity of the community in question.），而且从我们常用的两个生物多样性指数中，可以很轻易地推导出来：只要把 Shanon 熵的值（ 𝐻 ）取自然指数、把 Simpson 指数（ 𝐷 ）取倒数，就可以得到有效物种数。

最终Hills采用指数曲线的概念，将不同的多样性指数整合如下：

$$ ^qD=\left(\displaystyle\sum_{i=1}^{S} p_i^q\right)^{\frac{1}{1-q}}, q\in\mathbb{R} $$

其中，

q 值	Hills number	对应的原始多样性指数形式	原始多样性指数意义
0	$$^0D=S$$	$$S$$	物种数 S （相对侧重稀有种）
1	$$^1D=\displaystyle\lim_{q\to1}^qD=exp\left[-\sum_{i=1}^{s}p_i\ln p_i\right]=e^H$$	$$-\displaystyle\sum_{i=1}^{S} {p_i\ln{p_i}}$$	Shanon 熵 H
2	$$^2D=\frac{1}{D}\ (\frac{1}{\lambda})$$	$$\displaystyle\sum_{i=1}^{S} p_i^2$$	Simpson 指数 D (λ) （相对侧重常见种）

β多样性

β 多样性主要探讨在同时间的不同群集之间，或者某群集在不同时间点的差异有多大，因此许多量化群集间的差异程度（differentiation）、相似程度（similarity）、重复程度（overlap）或转换程度（turnover）方法被用以估计 β 多样性。

β 多样性估计量可以表示各个地区群集间的差异。与 α 多样性类似，β 多样性的评估大致上也分为只考虑物种数（richness）与同时考虑物种数与各物种个体充裕度（abundance）差异的估计量。好的 β 多样性估计量要具有单调性（monotonicity），在两个相同的的任一个群集中加入新的物种，β 多样性估计量值会上升；好的 β 多样性估计量也只和物种的相对数量有关，不因绝对数量的增减而有所不同。

只考虑丰富程度，包括

$$ Jaccard\ similarity\ index:\ S_j=\frac{S_{12}}{S_1+S_2-S_{12}}\\ $$ $$ Sørenson\ similarity\ index:\ S_ø=\frac{2S_{12}}{S_1+S_2}\\ $$ $$ Lenon\ similarity\ index:\ S_L=\frac{S_{12}}{S_{12}+min(S_1-S_{12},S_2-S_{12})} $$

其中S1是第一个群体中物种的数量，S2是第二个群体中物种的数量，S12是两个群体共有的物种的数量。

同时考虑丰富度与均匀度，Bray 与 Curtis (1957) 基于 Sørenson 相似度指数提出了量化方法：

$$ Bray-Curtis\ distance:\ C_{BC}=\frac{\displaystyle\sum_{i=1}^{S_{12}}min(x_i,y_i)}{\frac{1}{2}\left(\displaystyle\sum_{i=1}^{S_1}x_i+\displaystyle\sum_{i=1}^{S_2}y_i\right)} $$

xi与yi代表X与Y群集出现的第𝑖个物种个体数比率，当不考虑充裕度（abundance）时，此指数即等同于 Sørenson 相似度指数。

不同层次生物多样性估计量的分解

Jost针对三种多样性，整理出了 5 个重要的假设如下：

α 与 β 多样性彼此独立

在生态系统中，针对不同目标的估计值必须彼此独立，在这个前提下，α 与 β 多样性的大小不应该互相影响。
不同区域的生物多样性估计量可以互相比较

不管针对 α、β 或者 γ 多样性进行估计，不同区域的相同层次生物多样性估计量都要能够互相比较；相同的生物多样性估计量值也要可以描述相同的生物多样性程度。
α 多样性是各群集内多样性的平均值

如果一个区域内的所有群集 α 多样性都相同，那这个区域的 α 多样性估计量值也要维持相同；α 多样性就是该区域各群集的多样性在某种形式上的平均。
γ 须为 α、β 所决定

如同上个段落的生物多样性分解，在一区域中，α、β、γ 必然有著某种形式的关系，例如加法或乘法分解关系。
γ 必然大于 α 多样性

γ 多样性探讨区域内各物种的多样性，所包含的讯息不可能比 α 多样性的估计值还少。

依据该 5 项假设，Jost 利用 Hill number 搭配乘法分解，从 γ 与 α 多样性中分解出 β 多样性，表示如下：

$$ \begin{split} &^qD_\alpha=\left[\frac{\sum_{i=1}{S}p_{i1}^q+\sum_{i=1}{S}p_{i2}^q+...+\sum_{i=1}{S}p_{iN}^q} {N}\right]^{\frac{1}{1-q}}\\ &^qD_\gamma=\left[\displaystyle\sum_{i=1}^{S}\left(\frac{p_{i1}+p_{i2}+...p_{iN}} {N}\right)^q\right]^{\frac{1}{1-q}}\\ \ \\ &^qD_\beta={^qD_\gamma}/{^qD_\alpha}\\ \end{split} $$

其中pij表示群落j中物种i的相对丰富度；j=1,2,…,N; i=1,2,…,S，简单来说就是把每个群集中的每個物种的相对丰富度都列出来的意思。通过改变q的值，Jost与Chiu的这些指数可以转换为上文提到的几种β多样性指数。此外，由 β 多样性与群集的差异正相关，与群集相似度负相关，经过形式运算的转换与标准化后，另外得出转换—互补（turnover-complement）指数、同质性（homogeneity）指数与局部重复（local-overlap）指数：

$$ tunover-complement\ index:\ \frac{N-^qD_\beta}{N-1}\\ $$ $$ homogeneity\ index:\ \frac{1/^qD_\beta-1/N}{1-(1/N)}\\ $$ $$ local-overlap\ index:\ \frac{(1/^qD_\beta)^{q-1}-(1/N)^{q-1}}{1-(1-N)^{q-1}} $$

	转换-互补指数	同质性指数	局部重复指数	区域重复指数
q=0	Sørenson 相似度	Jaccard 相似度	Sørenson 相似度	Jaccard 相似度
q=1			Horn 重叠度	Horn 重叠度
q=2	区域重复指数	Morisita-Horn 重叠度	Morisita-Horn 重叠度	区域重复指数

Faith Phylogenetic Diversity谱系多样性

传统的生物多样性指数考虑的是物种的数量和组成差异，但是并未考虑到物种之间的亲缘关系。例如在传统多样性分析中，狸花猫和比格犬、狸花猫和缅因猫都算作两个物种，但是并未体现出物种之间的亲缘关系。然而事实上，前者的物种丰富度显然高于后者。为了刻画这种差异，谱系生物多样性的概念就引出来了。这个概念简单说来就是考虑了一个生境中不同的生物组分之间的亲缘关系，亲缘关系越接近，物种复杂度越低。

PD谱系多样性

把群集中调查到的物种做成一棵亲缘关系树，定义𝐿𝑖是每个支长（branch length），则PD就是所有支长的总和。如果只以生物分类法（taxonomy）来建构分类树，则每个分支的长度均为 1，这时候 𝑃𝐷就是这棵分类树的总节点数（以分类法建构出的多样性指数又称作支序多样性 cladistic diversity, CD）。此指数符合倍增性值。
$$ PD=\sum_{i=1}^{N}L_i $$

使用QIIME2进行多样性分析

QIIME 2的多样性分析使用q2-diversity插件，该插件支持计算α和β多样性指数、并应用相关的统计检验以及生成交互式可视化图表。我们将首先应用core-metrics-phylogenetic方法，该方法将FeatureTable[Frequency](特征表[频率])抽平到用户指定的测序深度，然后计算几种常用的α和β多样性指数，并使用Emperor为每个β多样性指数生成主坐标分析（PCoA）图。默认情况下计算的方法有：

α多样性
- 香农(Shannon’s)多样性指数（群落丰富度的定量度量，即包括丰富度richness和均匀度evenness两个层面）
- 可观测的OTU(Observed OTUs，群落丰富度的定性度量，只包括丰富度）
- Faith’s系统发育多样性（包含特征之间的系统发育关系的群落丰富度的定性度量）
- 均匀度Evenness（或 Pielou’s均匀度；群落均匀度的度量）
β多样性
- Jaccard距离（群落差异的定性度量，即只考虑种类，不考虑丰度）
- Bray-Curtis距离（群落差异的定量度量，较常用）
- 非加权UniFrac距离（包含特征之间的系统发育关系的群落差异定性度量）
- 加权UniFrac距离（包含特征之间的系统发育关系的群落差异定量度量）

需要提供给这个脚本的一个重要参数是--p-sampling-depth，它是指定重采样（即稀疏/稀疏rarefaction）深度。因为大多数多样指数对不同样本的不同测序深度敏感，所以这个脚本将随机地将每个样本的测序量重新采样至该参数值。例如，提供--p-sampling-depth 500，则此步骤将对每个样本中的计数进行无放回抽样，从而使得结果表中的每个样本的总计数为500。（例如，匹配到该样本额有3000条reads，则随机从中抽取500条进行计算）如果任何样本的总计数小于该值，那么这些样本将从多样性分析中删除。选择这个值很棘手。我们建议你通过查看上面创建的表table.qzv文件中呈现的信息并选择一个尽可能高的值（因此每个样本保留更多的序列）同时尽可能少地排除样本来进行选择。这里选择1103。

该操作会输出13个数据对象

core-metrics-results/faith_pd_vector.qza: Alpha多样性考虑进化的faith指数。
core-metrics-results/unweighted_unifrac_distance_matrix.qza: 无权重unifrac距离矩阵。
core-metrics-results/bray_curtis_pcoa_results.qza: 基于Bray-Curtis距离PCoA的结果。
core-metrics-results/shannon_vector.qza: Alpha多样性香农指数。
core-metrics-results/rarefied_table.qza: 等量重采样后的特征表。
core-metrics-results/weighted_unifrac_distance_matrix.qza: 有权重的unifrac距离矩阵。
core-metrics-results/jaccard_pcoa_results.qza: jaccard距离PCoA结果。
core-metrics-results/observed_otus_vector.qza: Alpha多样性observed otus指数。
core-metrics-results/weighted_unifrac_pcoa_results.qza: 基于有权重的unifrac距离的PCoA结果。
core-metrics-results/jaccard_distance_matrix.qza: jaccard距离矩阵。
core-metrics-results/evenness_vector.qza: Alpha多样性均匀度指数。
core-metrics-results/bray_curtis_distance_matrix.qza: Bray-Curtis距离矩阵。
core-metrics-results/unweighted_unifrac_pcoa_results.qza: 无权重的unifrac距离的PCoA结果。

以及4个可视化对象:

core-metrics-results/unweighted_unifrac_emperor.qzv：无权重的unifrac距离PCoA结果采用emperor可视化。
core-metrics-results/jaccard_emperor.qzv：jaccard距离PCoA结果采用emperor可视化。
core-metrics-results/bray_curtis_emperor.qzv：Bray-Curtis距离PCoA结果采用emperor可视化。
core-metrics-results/weighted_unifrac_emperor.qzv：有权重的unifrac距离PCoA结果采用emperor可视化。

1
2
3
4
5
6


time qiime diversity core-metrics-phylogenetic \
  --i-phylogeny rooted-tree.qza \
  --i-table table.qza \
  --p-sampling-depth 1103 \
  --m-metadata-file sample-metadata.tsv \
  --output-dir core-metrics-results

在计算多样性度量之后，我们可以开始在样本元数据的分组信息或属性值背景下探索样本的微生物组成差异。此信息存在于先前下载的示例元数据文件中。

我们将首先测试分类元数据列和alpha多样性数据之间的关系。我们将在这里为Faith系统发育多样性（群体丰富度的度量）和Evenness均匀度进行可视化操作。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#α多样性组间显著性分析和可视化
qiime diversity alpha-group-significance \
  --i-alpha-diversity core-metrics-results/faith_pd_vector.qza \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization core-metrics-results/faith-pd-group-significance.qzv

qiime diversity alpha-group-significance \
  --i-alpha-diversity core-metrics-results/evenness_vector.qza \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization core-metrics-results/evenness-group-significance.qzv

最后，排序是在样本元数据分组间探索微生物群落组成差异的流行方法。我们可以使用Emperor工具在示例元数据下探索主坐标分析（PCoA）绘图。虽然我们的core-metrics-phylogenetic命令已经生成了一些Emperor图，但我们希望传递一个可选的参数--p-custom-axes，这对于探索时间序列数据非常有用。采于core-metrics-phylogeny的PCoA结果也是一样的，这使得很容易与Emperor生成新的可视化。我们将采用未加权的UniFrac和Bray-Curtis的PCoA结果生成Emperor图，以便所得到的图将包含主坐标1、主坐标2和实验开始以来的天数(days since the experiment start)的轴。我们将使用最后一个轴来探索这些样本是如何随时间变化的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


qiime emperor plot \
  --i-pcoa core-metrics-results/unweighted_unifrac_pcoa_results.qza \
  --m-metadata-file sample-metadata.tsv \
  --p-custom-axes days-since-experiment-start \
  --o-visualization core-metrics-results/unweighted-unifrac-emperor-days-since-experiment-start.qzv

qiime emperor plot \
  --i-pcoa core-metrics-results/bray_curtis_pcoa_results.qza \
  --m-metadata-file sample-metadata.tsv \
  --p-custom-axes days-since-experiment-start \
  --o-visualization core-metrics-results/bray-curtis-emperor-days-since-experiment-start.qzv

α稀疏曲线

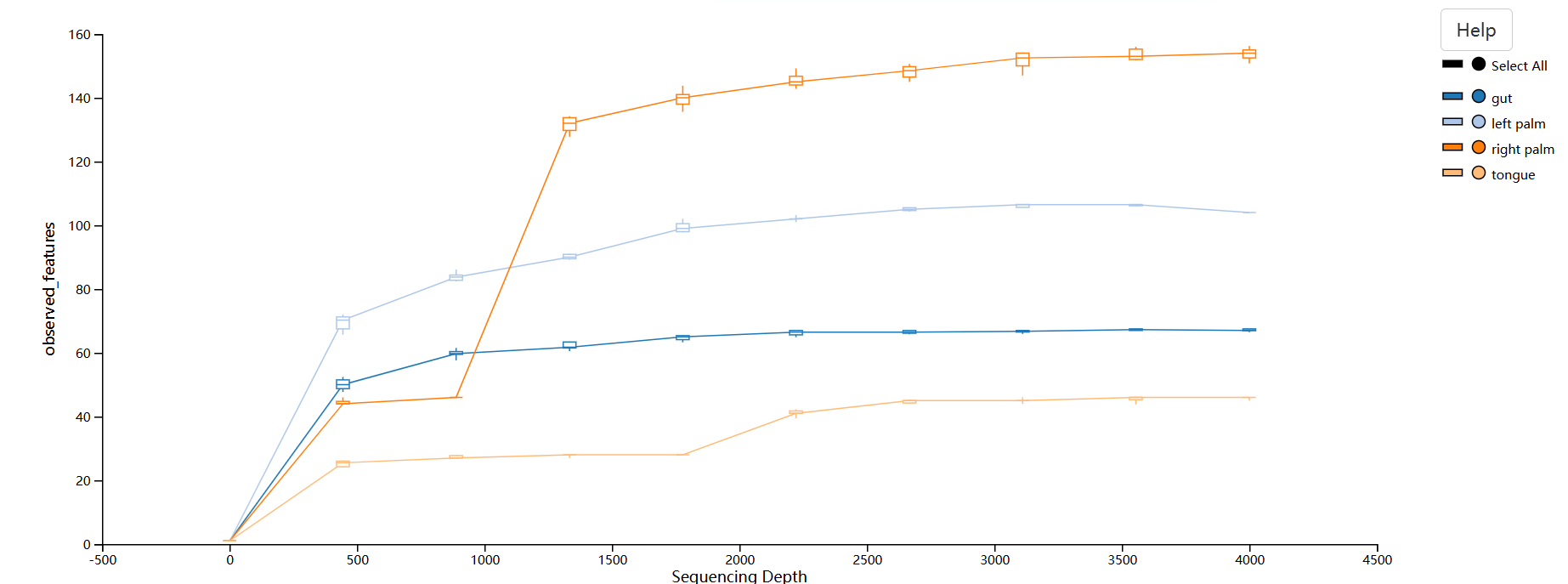
使用qiime diversity alpha-rarefaction可视化工具来探索α多样性与采样深度的关系。该可视化工具在多个采样深度处计算一个或多个α多样性指数，范围介于1（可选地--p-min-depth控制）和最大采样深度--p-max-depth提供值之间。在每个采样深度，将生成10个抽样表，并对表中的所有样本计算alpha多样性指数计算。迭代次数（在每个采样深度计算的稀疏表）可以通过--p-iterations来控制。在每个采样深度，将为每个样本绘制平均多样性值，如果提供样本元数据--m-metadata-file参数，则可以基于元数据对样本进行分组。

可视化将有两个图。顶部图是α稀疏图(rarefaction plot)，主要用于确定样品的丰度是否已被完全观察或测序。如果图中的线条在沿x轴的某个采样深度处看起来“平坦(level out)”（即斜率接近于零），这表明收集超过该采样深度的附加序列不太可能观测到新特征。如果绘图中的线条没有变平，这可能是因为尚未充分观察样本的丰富度（由于测序的序列太少），或者它可能是在数据中仍然存在许多测序错误（被误认为是新的多样性）。

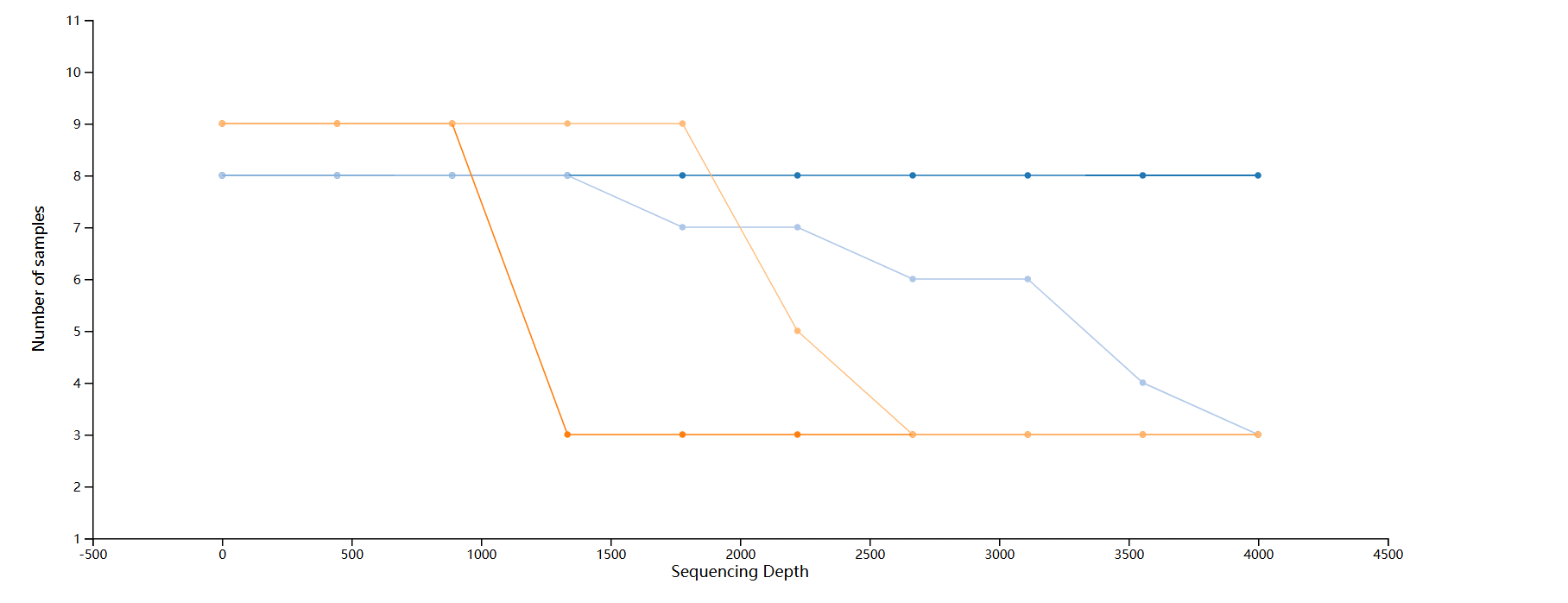
当通过元数据对样本进行分组时，此可视化中结果底部的绘图结果非常重要。它说明了当特征表被细化到每个采样深度时，每个组中剩余的样本数量。如果给定的采样深度d大于样本s的总频率(即，针对样本s获得的序列数)，则不可能计算采样深度d下样本s的多样性。在顶部绘图将不可靠，因为它将计算基于相对少的样本。因此，当通过元数据对样本进行分组时，必须查看底部图表，以确定顶部图表中显示的数据是否可靠的。

1
2
3
4
5
6


time qiime diversity alpha-rarefaction \
  --i-table table.qza \
  --i-phylogeny rooted-tree.qza \
  --p-max-depth 8000 \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization alpha-rarefaction.qzv

物种组成分析

OTU操作分类单元与ASV扩增子序列变体

在使用16S rRNA基因特定区域进行细菌鉴定时，我们面临两大挑战：（1）数据存在测序错误（噪音）；（2）数据可能无法实现种级（Species Level）水平的微生物鉴定。

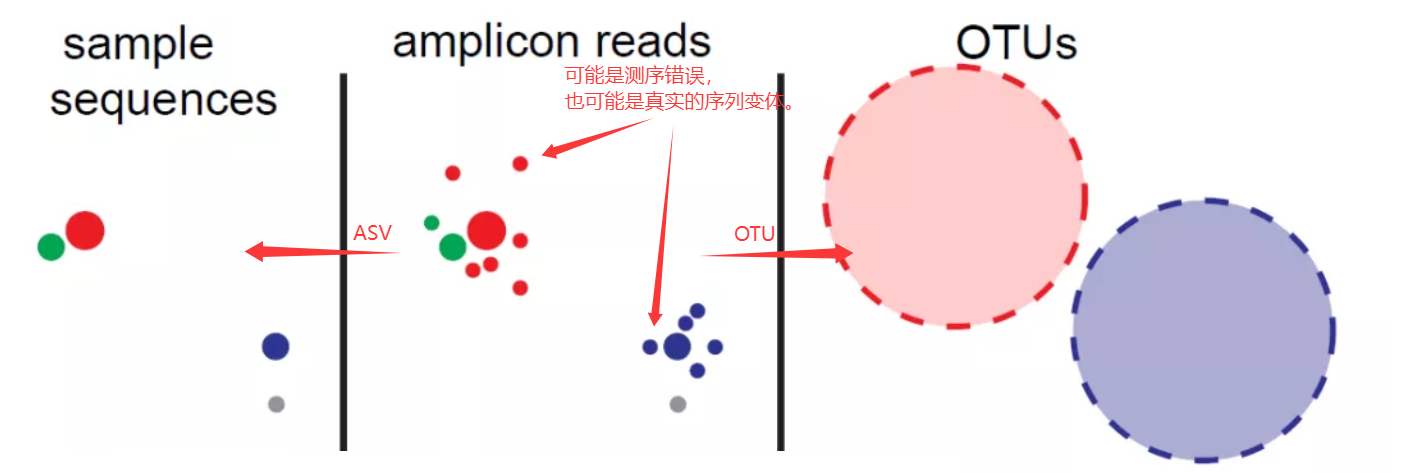
针对挑战一，当前主要通过两种主流方法消除噪音（源于PCR扩增和测序过程中的误差）：第一种是采用Mothur等工具对相似序列进行聚类，将其定义为操作分类单元（OTU）；第二种是采用dada2等平台构建统计学模型模拟误差，通过扩增子序列变体（ASVs）技术从噪音中还原真实序列。而对于挑战二，采用最新且经过严格质控的16S rRNA基因数据库可部分改善问题。但需要指出的是，某些分类群（如特定菌科）的16S rRNA基因可变区序列在种间高度保守，这种先天局限性使得该方法无法突破分类分辨率的天花板。要实现更高精度的分类鉴定，需结合其他技术手段进行补充分析。

OTU通过聚类（如层次聚类、UPARSE等），将超过相似度阈值的序列看成是一致的，并且选出一个代表序列来代表这些相似的序列。选择代表序列的方式包括以下几种：

中心序列（Centroid）：聚类中与其他序列相似度最高的序列。
最丰富序列（Most Abundant）：聚类中出现频率最高的序列。
从头生成共识序列（Consensus Sequence）：基于聚类内所有序列的碱基频率生成。

一个OTU的例子如下：序列ABC都是相似度在80%以上的序列，故聚类成一个OTU，其中第6位碱基和第10位碱基并不完全相同。其中第6位碱基中G出现了2次，C出现了1次，故选择G作为参考序列的第6位碱基。第10位也同理。这种操作相当与对测序结果进行“模糊处理”，虽然会损失一些测序精度，但是可以有效避免测序中的错误（噪音）导致的不正确的物种分类。

$$ SeqA:\ A\ T\ T\ G\ C\ G\ T\ A\ C A\\ SeqB:\ A\ T\ T\ G\ C\ G\ T\ A\ C\ T\\ SeqC:\ A\ T\ T\ G\ C\ C\ T\ A\ C\ A\\ RefS:\ A\ T\ T\ G\ C\ G\ T\ A\ C\ A $$

此外，ASV是另一种消除测序噪音的方法，通过机器学习的方式统计在特定质量值下，位点发生真实变异的概率$\lambda_{ij}$，判断序列$i$（扩增子）是否来自$j$（模板，丰度最高的序列）。之后再校正所有被判定为测序错误的位点，采用分裂分割算法（The divisive partitioning algorithm）进行最后的聚类：将所有序列作为一个partition，丰度最高的序列为中心，处于partition中的序列都与中心序列进行比较，计算丰度p值（p值是在位点变异率λij基础上计算获得整条序列是来自模板序列的可能性标准），当最小的p值小于阈值，则划分为新的partition，所有序列和新的中心序列进行比较，不断划分，直到不能再划分即所有序列都有与之对应的partition为止。这种聚类方式类似于以100%相似度进行聚类的OTU。

朴素贝叶斯分类器

朴素贝叶斯分类器是一种基于贝叶斯定理的简单概率分类器，其核心思想是通过特征的概率分布来预测类别。其采用了**“属性条件独立假设”（attribute conditional independent assumption）**，即各个特征之间是相互独立的。假设有如下训练集：

	特征i	分类
条目1
条目2
……
条目j	$X_{ji}=x_{ji}$	$Y_j=y$
……
条目M

训练过程

1、计算先验概率。分类为y的概率如下。其中:

$N_y$：训练集中类别为y的样本数。

$N$：总样本数。

$$ P(Y=y)=\frac{N_y}{N} $$

2、计算分类y的特征i的均值与标准差，并假设每个特征都服从高斯分布：

$\mu_{yi}$：分类为y时，特征i的均值。

$\sigma_{yi}$：分类为y时，特征i的标准差。

$$ P(x_i=k|Y=y)=\frac{1}{\sqrt{2\pi\sigma_{yi}^2}}e^{-\frac{(k-\mu_{yi})^2}{2\sigma_{yi}^2}} $$

预测过程

1、计算给定特征向量X时分类为y的条件概率：

$$ P(Y=y|X)=\frac{P(X|Y=y)P(Y=y)}{P(X)}\ ∝\ P(Y=y)\cdot\prod_{i=1}^nP(X_i|Y=y) $$

2、找到概率最大的分类：

$$ \hat Y=\arg \mathop{\min}\limits_{y}P(Y=y|X) $$

代码实现

使用已经训练好的分类器

这个过程的第一步是为FeatureData[Sequence]的序列进行物种注释。我们将使用经过Naive Bayes分类器预训练的，并由q2-feature-classifier插件来完成这项工作。这个分类器是在Greengenes 13_8 99% OTU上训练的，其中序列被修剪到仅包括来自16S区域的250个碱基，该16S区域在该分析中采用V4区域的515F/806R引物扩增并测序。我们将把这个分类器应用到序列中，并且可以生成从序列到物种注释结果关联的可视化。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


# 下载预训练的分类器
wget \
  -O "gg-13-8-99-515-806-nb-classifier.qza" \
  "https://docs.qiime2.org/2024.2/data/tutorials/moving-pictures-usage/gg-13-8-99-515-806-nb-classifier.qza"

# 指定分类器和特征表进行分类
qiime feature-classifier classify-sklearn \
  --i-classifier gg-13-8-99-515-806-nb-classifier.qza \
  --i-reads rep-seqs.qza \
  --o-classification taxonomy.qza

qiime metadata tabulate \
  --m-input-file taxonomy.qza \
  --o-visualization taxonomy.qzv
  
# 将结果以条形图的形式来展示
qiime taxa barplot \
  --i-table table.qza \
  --i-taxonomy taxonomy.qza \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization taxa-bar-plots_pretrained.qzv

训练自己的分类器

如果不使用他人已经训练好的分类器，还可以自行进行分类器的训练。

这里我们使用85_otus.fasta(按85%相似度聚类)的文件用于演示，是因为体积小运行更快。实际中大家一般使用参考序列99%和97%聚类的结果用于分类。如果电脑或服务器配置太低无法运行，可选择更低聚类的结果文件用于分析。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


# 创建工作目录
mkdir -p training-feature-classifiers
cd training-feature-classifiers

# 下载参考OTU数据集
wget \
  -O "85_otus.fasta" \
  "https://data.qiime2.org/2019.7/tutorials/training-feature-classifiers/85_otus.fasta"

# 下载参考数据集的物种分类信息
wget \
  -O "85_otu_taxonomy.txt" \
  "https://data.qiime2.org/2019.7/tutorials/training-feature-classifiers/85_otu_taxonomy.txt"

接下来，我们将这些数据导入到QIIME 2对象中。由于Greengenes序列物种注释文件（85_otu_Taxonomy.txt）是一个不带标题的制表符分隔文件（tsv），因此必须指定HeaderlessTSVTaxonomyFormat作为源格式，因为默认源格式需要标题。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


# 导入参考序列
qiime tools import \
  --type 'FeatureData[Sequence]' \
  --input-path 85_otus.fasta \
  --output-path 85_otus.qza

# 导入物种分类信息
qiime tools import \
  --type 'FeatureData[Taxonomy]' \
  --input-format HeaderlessTSVTaxonomyFormat \
  --input-path 85_otu_taxonomy.txt \
  --output-path ref-taxonomy.qza

2012年Werner等人研究表明，当一个朴素贝叶斯(Naive Bayes)分类器只训练被测序的目标序列的区域时，16S rRNA基因序列的分类准确度会提高。这种策略不一定对其他标记基因同样有效。我们试图对序列进行分类的是120个碱基的单端序列，这些读长是用515F/806R引物对16S rRNA基因序列进行扩增的产物。我们在这里通过从参考数据库中提取基于与该对引物匹配的区域，然后将结果截取至120个碱基来对此进行优化。

注释：-p-trunc-len参数只能用于比对序列被剪裁成相同长度或更短的长度时，才需要剪裁参考序列。成功双端合并序列的长度通常是可变的。未在特定长度截断的单端读取的长度也可能是可变的。对于双端和未经修剪的单端读的物种分类，我们建议对在适当的引物位置提取但不修剪为等长的序列进行分类器训练。

注释：用于提取扩增区域的引物序列应该是包含在引物结构中的实际DNA结合（即生物）序列。它不应包含任何非生物、非匹配的序列，例如接头、连接物或条形码序列。如果你不确定你的引物序列的哪个部分是真正的DNA结合区域，你应该咨询为你构建测序文库的工程师，你选择的测序中心，或者这些引物的原始文献。如果你的引物序列长度大于30nt，它们很可能包含一些非生物序列。

注释：上面的示例命令使用min-length和max-length参数，来排除使用这些引物远远超出预期长度分布的模拟扩增结果。这样的扩增产物可能是非特异性扩增，应该排除。如果您将此命令调整为自己的项目中使用，请确保选择适合标记基因，而不是此处使用序列或参数。min-length参数在trim-left和trunc-len参数之后应用，在max-length之前应用，因此一定要设置适当的设置，以防止有效序列被过滤掉。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


# 按我们测序的引物来提取参考序列中的一段，并将结果剪裁至120bp长度。
qiime feature-classifier extract-reads \
  --i-sequences 85_otus.qza \
  --p-f-primer GTGCCAGCMGCCGCGGTAA \
  --p-r-primer GGACTACHVGGGTWTCTAAT \
  --p-trunc-len 120 \
  --p-min-length 100 \
  --p-max-length 400 \
  --o-reads ref-seqs.qza
  
# 基于筛选的指定区段，生成实验特异的分类集
time qiime feature-classifier fit-classifier-naive-bayes \
  --i-reference-reads ref-seqs.qza \
  --i-reference-taxonomy ref-taxonomy.qza \
  --o-classifier classifier.qza

#使用训练好的分类器进行物种注释
cd ..

time qiime feature-classifier classify-sklearn \
  --i-classifier training-feature-classifiers/classifier.qza \
  --i-reads rep-seqs.qza \
  --o-classification taxonomy.qza

qiime metadata tabulate \
  --m-input-file taxonomy.qza \
  --o-visualization taxonomy_MyClassifier.qzv
  
# 将结果以条形图的形式来展示
qiime taxa barplot \
  --i-table table.qza \
  --i-taxonomy taxonomy.qza \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization taxa-bar-plots_MyClassifier.qzv
  

使用Greengenes2最新的数据库

Greengenes2是一个适用于短读长宏基因组测序和16S rRNA测序研究的统一系统发育树和分类体系。它能够直接整合16S rRNA和宏基因组测序数据集。此外还保留了GTDB（Genome Taxonomy Database）的分类注释，包括其多系分类标签。对于专注于16S rRNA基因V4区域的研究，分类可以直接从系统发育树中推导，而无需使用朴素贝叶斯（Naive Bayes）方法，这似乎能够提供比朴素贝叶斯更高分辨率的分类结果。

对于V4测序数据，无需训练或使用分类器，直接将特征表（FeatureTable[Frequency]）和数据库取交集即可。Greengenes2的片段放置部分主要基于Qiita默认处理流程中的EMP（Earth Microbiome Project） 16S 515F引物，因此包含90、100和150bp的ASV。因此对数据库取交集之前需要把代表性序列修剪为90、100或150bp。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


pip install q2-greengenes2
pip install redbiom

# 下载数据库
wget http://ftp.microbio.me/greengenes_release/2022.10/2022.10.taxonomy.asv.nwk.qza
# 如果特征表中特征是以MD5值存储的，下载对应的MD5值版本的数据库
wget http://ftp.microbio.me/greengenes_release/2022.10/2022.10.taxonomy.md5.nwk.qza

# 在去噪这一步将序列修建为90bp长度（或100bp、150bp，但不能是其它值）
time qiime dada2 denoise-single \
  --i-demultiplexed-seqs demux.qza \
  --p-trim-left 0 \
  --p-trunc-len 90 \
  --o-representative-sequences rep-seqs_90.qza \
  --o-table table_90.qza \
  --o-denoising-stats stats_90.qza

# 使用数据库对特征表进行过滤
qiime greengenes2 filter-features \
    --i-feature-table table_90.qza \
    --i-reference 2022.10.taxonomy.md5.nwk.qza \
    --o-filtered-feature-table table_90_gg2.qza

# 从数据库中获取对应的物种分类信息
qiime greengenes2 taxonomy-from-table \
    --i-reference-taxonomy 2022.10.taxonomy.md5.nwk.qza \
    --i-table table_90_gg2.qza \
    --o-classification table_90_gg2.taxonomy.qza

qiime metadata tabulate \
  --m-input-file table_90_gg2.taxonomy.qza \
  --o-visualization table_90_gg2.taxonomy.qzv
  
# 可视化，bar-plot
qiime taxa barplot \
  --i-table table_90_gg2.qza \
  --i-taxonomy table_90_gg2.taxonomy.qza \
  --m-metadata-file sample-metadata.tsv \
  --o-visualization taxa-bar-plots_V4Map.qzv

而对于非V4区域测序结果，建议使用non-v4-16s操作，它将使用q2-vsearch对Greengenes2中的全长16S序列执行闭参考OTU挑选（closed reference OTU picking）。详情可见Introducing Greengenes2 2022.10 - Community Contributions - QIIME 2 Forum。

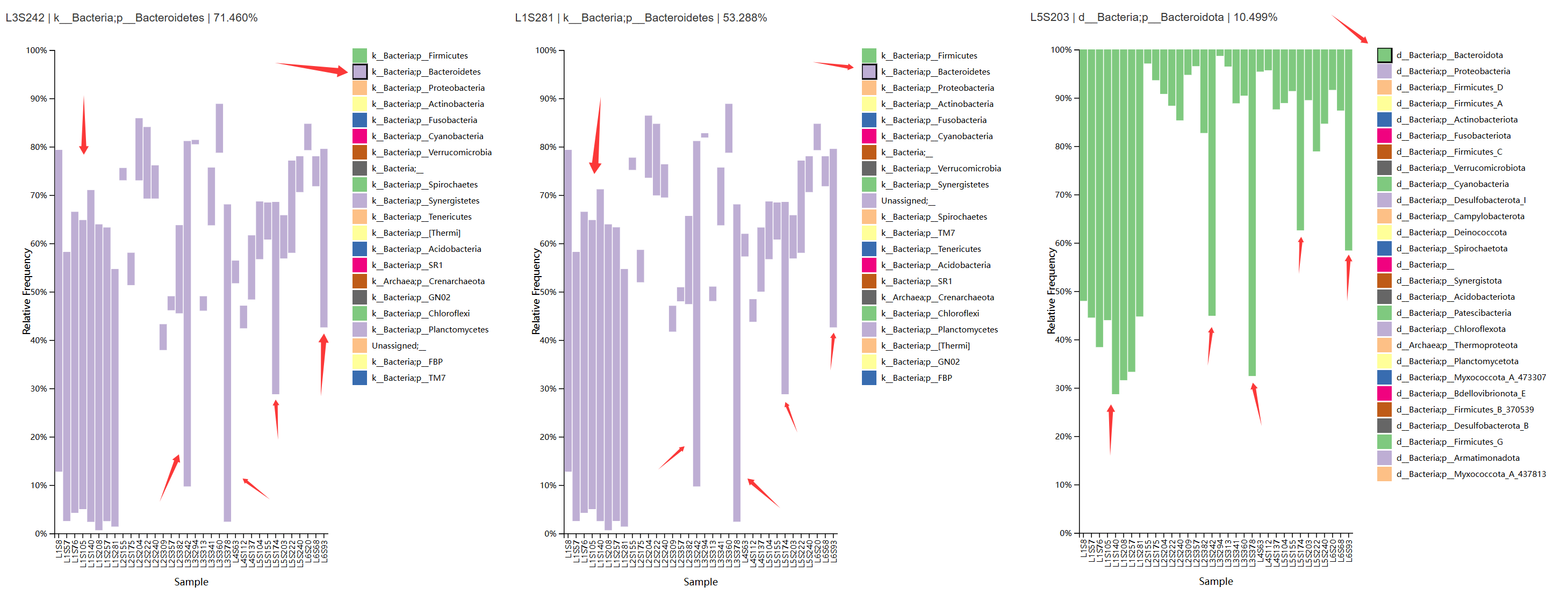
三种物种组成分析方法的一致性

以下三个图片分别为预训练的分类器、自己训练的分类器以及使用GreenGenes2数据库对特征表直接取交集的结果。这里选择了Level2水平的物种组成，横坐标按样本id排序，并且选择拟杆菌属结果进行显示（前两个是k_Bacteria;p_Bacteroidetes，第三个是d_Bacteria;p_Bacteroidota）,其分析结果趋于一致。例如，对于该菌属，三种方法均得出了L1S8-L1S281，以及L3S242、L3S378、L5S174、L6S93样本相对丰度较高的结果。

注：物种分类的层次包括：域（Domain）、界（Kingdom）、门（Phylum）、纲（Class）、目（Order）、科（Family）、属（Genus）、种（Species）

d9f0883e-967c-48fd-ac8c-76aa9770019a

ANCOM差异丰度分析

ANCOM可用于识别不同样本组中丰度差异的特征。ANCOM是在q2-composition插件中实现的。ANCOM假设很少（小于约25%）的特征在组之间改变。如果你期望在组之间有更多的特性正在改变，那么就不应该使用ANCOM，因为它更容易出错（I类/假阴性和II类/假阳性错误都有可能增加）。因为我们预期身体各部位之间的许多特征都会发生变化，所以在本教程中，我们将过滤完整的特征表后只包含肠道样本。然后，我们将应用ANCOM来确定哪种（如果有的话）序列变体在我们两个受试者的肠道样本中丰度存在差异。

我们将首先创建一个只包含肠道样本的特征表。

1
2
3
4
5


qiime feature-table filter-samples \
  --i-table table.qza \
  --m-metadata-file sample-metadata.tsv \
  --p-where "[body-site]='gut'" \
  --o-filtered-table gut-table.qza

ANCOM基于每个样本的特征频率对FeatureTable[Composition]进行操作，但是不能容忍零。为了构建组成composition 对象，必须提供一个添加伪计数add-pseudocount（一种遗失值插补方法）的FeatureTable[Frequency]对象，这将产生FeatureTable[Composition]对象。

1
2
3


qiime composition add-pseudocount \
  --i-table gut-table.qza \
  --o-composition-table comp-gut-table.qza

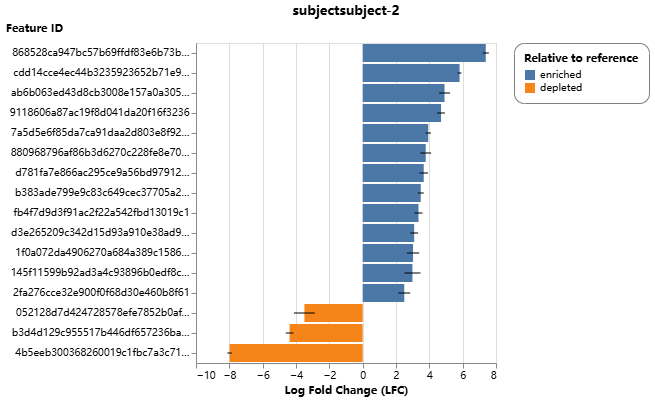
接下来可用ANCON对两组的特征进行丰度差异的比较了。（以“Subject”为分组依据，显示的是Subject2相对于Subject1的结果。）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


qiime composition ancombc \
  --i-table gut-table.qza \
  --m-metadata-file sample-metadata.tsv \
  --p-formula 'subject' \
  --o-differentials ancombc-subject.qza

qiime composition da-barplot \
  --i-data ancombc-subject.qza \
  --p-significance-threshold 0.001 \
  --o-visualization da-barplot-subject.qzv

visualization